题目内容
如图1,将 EAF绕着四边形ABCD的顶点A顺时针旋转,
EAF绕着四边形ABCD的顶点A顺时针旋转, EAF的两边分别与DC的延长线交于点F,与CB的延长线交于点E,连接EF。
EAF的两边分别与DC的延长线交于点F,与CB的延长线交于点E,连接EF。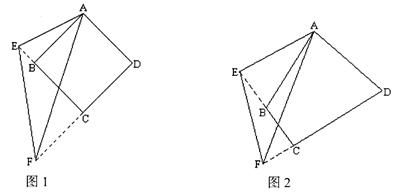
【小题1】若四边形ABCD为正方形,当 EAF=
EAF=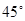 时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)
时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)
【小题2】如图2,如果四边形ABCD中,AB=AD, ABC与
ABC与 ADC互补,当
ADC互补,当 EAF=
EAF= 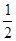
 BAD时,EF与DF、BE之间有怎样的数量关系?请写出它们之间的关系式并给予证明。
BAD时,EF与DF、BE之间有怎样的数量关系?请写出它们之间的关系式并给予证明。
【小题3】在(2)中,若BC=4,DC=7,CF=2,求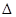 CEF的周长(直接写出结果即可)。
CEF的周长(直接写出结果即可)。
【小题1】EF=DF-BE
【小题2】EF=DF-BE。
证明:在DF上截取DM=BE,连接AM。如图,
∵ D+
D+ ABC=
ABC= ABE+
ABE+ ABC=
ABC= ,
,
∴ D=
D= ABE。
ABE。
∵AD=AB,
∴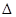 ADM≌
ADM≌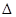 ABE。
ABE。
∴AM=AE, DAM=
DAM= BAE。
BAE。
∵ EAF=
EAF= BAE+
BAE+ BAF=
BAF=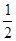
 BAD,
BAD,
∴ DAM+
DAM+ BAF=
BAF=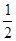
 BAD。
BAD。
∴ MAF=
MAF=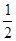
 BAD。
BAD。
∴ EAF=
EAF= MAF。
MAF。
∵AF是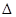 EAF与
EAF与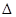 MAF的公共边,
MAF的公共边,
∴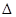 EAF≌
EAF≌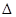 MAF。
MAF。
∴EF=MF。
∵MF=DF-DM=DF-BE,
∴EF=DF-BE。
【小题3】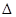 CEF的周长为15。
CEF的周长为15。
解析

练习册系列答案
相关题目

 时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)
时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)
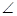 EAF绕着四边形ABCD的顶点A顺时针旋转,
EAF绕着四边形ABCD的顶点A顺时针旋转,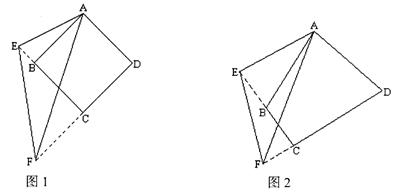
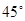 时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)
时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)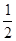
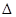 CEF的周长(直接写出结果即可)。
CEF的周长(直接写出结果即可)。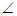 EAF绕着四边形ABCD的顶点A顺时针旋转,
EAF绕着四边形ABCD的顶点A顺时针旋转,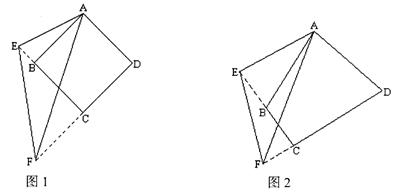
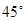 时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)
时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)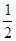
 CEF的周长(直接写出结果即可)。
CEF的周长(直接写出结果即可)。