题目内容
如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )

A.30° B.45° C.60° D.90°
B【考点】等腰三角形的性质.
【专题】计算题.
【分析】根据等腰三角形两底角相等求出∠ABC=∠ACB,再求出∠CBD,然后根据∠ABD=∠ABC﹣∠CBD计算即可得解.
【解答】解:∵AB=AC,∠A=30°,
∴∠ABC=∠ACB= (180°﹣∠A)=
(180°﹣∠A)= (180°﹣30°)=75°,
(180°﹣30°)=75°,
∵以B为圆心,BC的长为半径圆弧,交AC于点D,
∴BC=BD,
∴∠CBD=180°﹣2∠ACB=180°﹣2×75°=30°,
∴∠ABD=∠ABC﹣∠CBD=75°﹣30°=45°.
故选:B.

【点评】本题考查了等腰三角形的性质,主要利用了等腰三角形两底角相等,熟记性质是解题的关键.

练习册系列答案
相关题目
 有意义;
有意义;


 B.
B.
 C.
C.


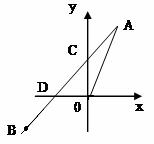 (1)求一次函数的解析式;
(1)求一次函数的解析式;