题目内容
将边长为1的正方形ABCD绕A点按逆时针方向旋转60°，至正方形AB′C′D′，则旋转前后两个正方形重叠部分的面积为分析：连接AM，设DM=x，可得∠MAD=15°，由三角函数的定义可得AM=
，根据勾股定理构造方程
为x2+1=（
）2，解可得DM即x的值，进一步计算可得重叠部分的面积．
| x |
| sin15° |
为x2+1=（
| x |
| sin15° |
解答：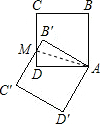
解：连接AM，设DM=x，
则∠MAD=15°，AM=
，
有x2+1=（
）2，
解得x=2-
，
所以重叠部分的面积SADMB′=2-
，
故答案为2-
．
解：连接AM，设DM=x，则∠MAD=15°，AM=
| x |
| sin15° |
有x2+1=（
| x |
| sin15° |
解得x=2-
| 3 |
所以重叠部分的面积SADMB′=2-
| 3 |
故答案为2-
| 3 |
点评：本题考查旋转的性质：旋转变化前后，对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等．要注意旋转的三要素：①定点-旋转中心；②旋转方向；③旋转角度．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
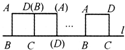将边长为8cm的正方形ABCD的四边沿直线l向右滚动（不滑动），当正方形滚动两周时，正方形的顶点A所经过的路线的长是（ ）A、（4
| ||
B、（8
| ||
C、（8
| ||
D、（4
|
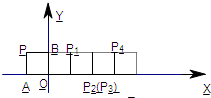18、如图，将边长为1的正方形OAPB沿x轴正方向连续翻转2008次，点P依次落在点P1，P2，P3，…，P2008的位置，则P2008的横坐标X2008=
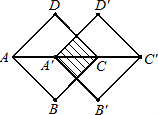如图，将边长为
如图，将边长为12cm的正方形纸片ABCD折叠，使得点A落在边CD上的E点，折痕为MN．若CE的长为8cm，则MN的长为（ ）
将边长为4的正方形在如图的平面直角坐标系中．点P是OA上的一个动点，且从点O向点A运动．连接CP交对角线OB于点D，连接AD．