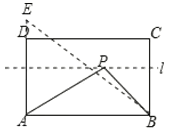
题目内容
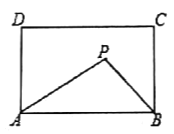
【题目】如图所示，在矩形
中，
，
，矩形内部有一动点
满足
，则点到
，
两点的距离之和
的最小值为（ ）.
A.
B.
C.
D.
【答案】D
【解析】
首先由
，得出动点P在与AB平行且与AB的距离是2的直线l上，作A关于直线l的对称点E，连接AE，连接BE，则BE的长就是所求的最短距离．然后在直角三角形ABE中，由勾股定理求得BE的值，即PA＋PB的最小值．
解：设△ABP中AB边上的高是h．
∵，
∴
ABh＝
ABAD，
∴h＝
AD＝2，
∴动点P在与AB平行且与AB的距离是2的直线l上，如图，作A关于直线l的对称点E，连接AE，BE，则BE的长就是所求的最短距离．
在Rt△ABE中，∵AB＝4，AE＝2＋2＝4，
∴BE＝
，
即PA＋PB的最小值为
．
故选：D．
练习册系列答案
优加精卷系列答案
相关题目
