题目内容
10.用适当的方法解方程(1)x2+x-12=0
(2)2x(x-3)-1=0
(3)2(2t+3)2=3(2t+3)
(4)(x+4)2-(2x-1)2=0.
分析 (1)利用十字相乘法将方程左边的多项式分解因式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到原方程的解.
(2)把已知方程转化为一般式方程,然后利用求根公式解答;
(3)把2t+3看成整体进行因式分解,从而求解;
(4)方程左边利用平方差公式分解后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
解答 解:(1)x2+x-12=0,
分解因式得:(x-3)(x+4)=0,
可得x-3=0或x+4=0,
解得:x1=3,x2=-4.
(2)由原方程,得
2x2-6x-1=0,
则a=2,b=-6,c=-1,
所以△=b2-4ac=(-6)2-4×2×(-1)=44,
所以x=$\frac{6±2\sqrt{11}}{4}$=$\frac{3±\sqrt{11}}{2}$,
解得:x1=$\frac{3+\sqrt{11}}{2}$,x2=$\frac{3-\sqrt{11}}{2}$;
(3)2(2t+3)2=3(2t+3),
原方程化为:(2t+3)[2(2t+2)-3]=0,
t1=-$\frac{3}{2}$,t2=-$\frac{1}{4}$;
(4)(x+4)2-(2x-1)2=0.
分解因式得:(x+4+2x-1)(x+4-2x+1)=0,
即(3x+3)(-x+5)=0,
解得:x1=-1,x2=5.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
1.⊙O内一点M到圆的最大距离为10cm,最短距离为8cm,那么过M点的最短弦长为( )
| A. | 1cm | B. | 8$\sqrt{5}$cm | C. | $\sqrt{41}$cm | D. | 9cm |
2.若a<$\sqrt{20}$<b,其中a,b是两个连续的整数,则a+b=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
18.已知方程(x+3)2=5(x+3),则该方程用因式分解法可化简为( )
| A. | (x+3)(x+5)=0 | B. | (x+3)(x+2)=0 | C. | (x+3)(x-5)=0 | D. | (x+3)(x-2)=0 |
 如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别是点D,E,则PE=PD(图中相等的线段,只写一对)
如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别是点D,E,则PE=PD(图中相等的线段,只写一对)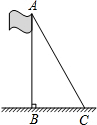 数学综合实验课上,同学们在测量学校旗杆的高度的时候发现:将旗杆顶端升旗用的绳子垂到地面还多2米,当把绳子的下端拉开8米后,下端刚好接触到地面,且绳子处于绷直状态.根据以上数据,计算旗杆的高度和升旗用的绳子的长度.
数学综合实验课上,同学们在测量学校旗杆的高度的时候发现:将旗杆顶端升旗用的绳子垂到地面还多2米,当把绳子的下端拉开8米后,下端刚好接触到地面,且绳子处于绷直状态.根据以上数据,计算旗杆的高度和升旗用的绳子的长度.