题目内容
如图，已知D、E为△ABC的边AB、AC上的点，BE⊥AC，CD⊥AB，BE、DC相交于点O，则图中相似三角形对数为（ ）| A、4 | B、6 | C、8 | D、10 |
分析：根据相似三角形判定定理：两角对应相等的两三角形相似，对应边成比例且夹角相等的两三角形相似，即可判断．
解答：解：∵BE⊥AC，CD⊥AB，
∴∠ADC=∠AEB=90°，
又∵∠A为公共角，
∴△ABE∽△ACD；
同理△BDO∽△CEO，△CEO∽△CDA，
∵△ABE∽△ACD，
∴
=
，
∴
=
，
∵∠A=∠A，
∴△ADE∽△ACB，
同理可证，△BDO∽△CEO，
=
，
又∵∠DOE=∠BOC
∴△DOE∽△COB．
∵△ABE∽△ACD，△OBD∽△ABE，△OCE∽△ACD，
∴根据相似三角形具有传递性得出△ODB∽△ADC，△OEC∽△AEB，
即相似三角形共8对，
故选C．
∴∠ADC=∠AEB=90°，
又∵∠A为公共角，
∴△ABE∽△ACD；
同理△BDO∽△CEO，△CEO∽△CDA，
∵△ABE∽△ACD，
∴
| AE |
| AD |
| AB |
| AC |
∴
| AD |
| AC |
| AE |
| AB |
∵∠A=∠A，
∴△ADE∽△ACB，
同理可证，△BDO∽△CEO，
| OE |
| OD |
| OC |
| OB |
又∵∠DOE=∠BOC
∴△DOE∽△COB．
∵△ABE∽△ACD，△OBD∽△ABE，△OCE∽△ACD，
∴根据相似三角形具有传递性得出△ODB∽△ADC，△OEC∽△AEB，
即相似三角形共8对，
故选C．
点评：此题主要考查学生对相似三角形判定定理的理解和掌握，这是今后进一步学习相似三角形有关知识的基础，要求学生熟练掌握．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
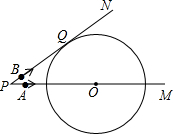P出发，点A以5cm/s的速度沿射线PM方向运动，点B以4cm/s的速度沿射线PN方向运动．设运动时间为ts．
如图，已知E、F分别为矩形ABCD的边BA、DC的延长线上的点，且AE=
如图，已知⊙P的半径为1，圆心P在抛物线
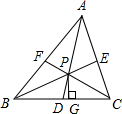如图，已知△ABC，P为内角平分线AD，BE，CF的交点，过点P作PG⊥BC于G，试说明∠BPD与∠CPG的大小关系，并说明理由．
如图，已知长方形的长为a，宽为b，且a＞b，则阴影部分的面积用代数式表示为