题目内容
(1)当a<0时,化简 ;
;
(2)已知x满足的条件为 ,化简
,化简 ;
;
(3)实数a,b在数轴上表示如图,化简: .
.

解:(1)∵a<0,
∴a-1<0,
原式=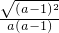 =
= =
=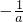 ;
;
(2)解不等式 得-1<x<3,
得-1<x<3,
∴原式= ,
,
∵-1<x<3,
∴x-3<0,x+1>0,
∴原式=3-x+x+1=4;
(3)观察数轴可得b<-2,1<a<2,
∴a+2>0,b-2<0,a+b<0,
∴原式=a+2-(2-b)+(-a-b),
=0.
分析:(1)先把式子化为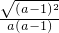 ,根据a的取值范围,再开根号,约去公因式即得结果.
,根据a的取值范围,再开根号,约去公因式即得结果.
(2)先解不等式,得出x的取值范围,再开根号,合并同类项即得结果;
(3)先由a,b在数轴上的位置,得出a,b的取值范围,再开根号,合并同类项即得结果.
点评:本题考查二次根式的化简,解答本题关键是要会用二次根式的性质 =|a|,根据字母的范围去绝对值.
=|a|,根据字母的范围去绝对值.
∴a-1<0,
原式=
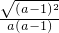 =
= =
=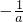 ;
;(2)解不等式
 得-1<x<3,
得-1<x<3,∴原式=
 ,
,∵-1<x<3,
∴x-3<0,x+1>0,
∴原式=3-x+x+1=4;
(3)观察数轴可得b<-2,1<a<2,
∴a+2>0,b-2<0,a+b<0,
∴原式=a+2-(2-b)+(-a-b),
=0.
分析:(1)先把式子化为
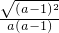 ,根据a的取值范围,再开根号,约去公因式即得结果.
,根据a的取值范围,再开根号,约去公因式即得结果.(2)先解不等式,得出x的取值范围,再开根号,合并同类项即得结果;
(3)先由a,b在数轴上的位置,得出a,b的取值范围,再开根号,合并同类项即得结果.
点评:本题考查二次根式的化简,解答本题关键是要会用二次根式的性质
 =|a|,根据字母的范围去绝对值.
=|a|,根据字母的范围去绝对值. 
练习册系列答案
相关题目
当x<3时,化简代数式
的结果是( )
| x2-6x+9 |
| A、x+3 | B、-x-3 |
| C、x-3 | D、3-x |
当x>2时,化简
+2,得( )
| (2-x)2 |
| A、x | B、x-4 |
| C、4+x | D、4-x |
已知下列运算中,正确的是( )
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、当a<0时,化简:
|