题目内容
已知,AB是⊙O的直径,AB=8,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,PC=5,PT为⊙O的切线,切点为T.(1)如图(1),当C点运动到O点时,求PT的长;
(2)如图(2),当C点运动到A点时,连接PO、BT,求证:PO∥BT;
(3)如图(3),设PT2=y,AC=x,求y与x的函数关系式及y的最小值.

【答案】分析:(1)连接OT,根据题意,由勾股定理可得出PT的长;
(2)连接OT,则OP平分劣弧AT,则∠AOP=∠B,从而证出结论;
(3)设PC交⊙O于点D,延长线交⊙O于点E,由相交弦定理,可得出CD的长,再由切割线定理可得出y与x之间的关系式,进而求得y的最小值.
解答: (1)解:连接OT
(1)解:连接OT
∵PC=5,OT=4,
∴由勾股定理得,PT= =
= =3;
=3;
(2)证明:连接OT,∵PT,PC为⊙O的切线,
∴OP平分劣弧AT,
∴∠POA=∠POT,
∵∠AOT=2∠B,
∴∠AOP=∠B,
∴PO∥BT;
(3)解:设PC交⊙O于点D,延长线交⊙O于点E,
由相交弦定理,得CD2=AC•BC,
∵AC=x,∴BC=8-x,
∴CD= ,
,
∴由切割线定理,得PT2=PD•PE,
∵PT2=y,PC=5,
∴y=[5- ][5+
][5+ ],
],
∴y=25-x(8-x)=x2-8x+25,
∴y最小= =9.
=9.
点评:本题是一道综合题,考查了切线的性质、二次函数的最值以及勾股定理的内容,是中考压轴题,难度较大.
(2)连接OT,则OP平分劣弧AT,则∠AOP=∠B,从而证出结论;
(3)设PC交⊙O于点D,延长线交⊙O于点E,由相交弦定理,可得出CD的长,再由切割线定理可得出y与x之间的关系式,进而求得y的最小值.
解答:
 (1)解:连接OT
(1)解:连接OT∵PC=5,OT=4,
∴由勾股定理得,PT=
 =
= =3;
=3;(2)证明:连接OT,∵PT,PC为⊙O的切线,
∴OP平分劣弧AT,
∴∠POA=∠POT,
∵∠AOT=2∠B,
∴∠AOP=∠B,
∴PO∥BT;
(3)解:设PC交⊙O于点D,延长线交⊙O于点E,
由相交弦定理,得CD2=AC•BC,
∵AC=x,∴BC=8-x,
∴CD=
 ,
,∴由切割线定理,得PT2=PD•PE,
∵PT2=y,PC=5,
∴y=[5-
 ][5+
][5+ ],
],∴y=25-x(8-x)=x2-8x+25,
∴y最小=
 =9.
=9.点评:本题是一道综合题,考查了切线的性质、二次函数的最值以及勾股定理的内容,是中考压轴题,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•钦州)如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:
(2013•钦州)如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1: 如图,在平面直角坐标系中,直
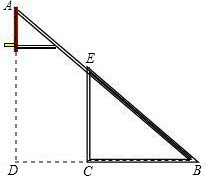
如图,在平面直角坐标系中,直 红星中学篮球课外活动小组的同学自己动手制作一副简易篮球架.如图,是篮球架的侧面示意图,已知篮板所在直线AD和直杆EC都与BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜杆AB与直杆EC的长分别是多少米?(计算结果精确到0.01米,参考数据:(sin40°≈0.588,cos40°≈0.809,tan40°≈0.727.)
红星中学篮球课外活动小组的同学自己动手制作一副简易篮球架.如图,是篮球架的侧面示意图,已知篮板所在直线AD和直杆EC都与BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜杆AB与直杆EC的长分别是多少米?(计算结果精确到0.01米,参考数据:(sin40°≈0.588,cos40°≈0.809,tan40°≈0.727.)