题目内容
 在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.(1)求tan∠FOB的值;
(2)用含t的代数式表示△OAB的面积S.
考点:相似三角形的判定与性质,坐标与图形性质,正方形的性质
专题:
分析:(1)已知点A的坐标,可推出CD=OD=DE=EF=t,可求出tan∠FOB.
(2)证明△ACF∽△AOB推出:
=
,然后求出OB关于t的等量关系式,继而求出S△OAB的值.
(2)证明△ACF∽△AOB推出:
2
| ||||
2
|
| t |
| OB |
解答:解:(1)∵A(2,2),
∴∠AOB=45°,
∴CD=OD=DE=EF=t,
∴tan∠FOB=
=
;
(2)∵CF∥OB,
∴△ACF∽△AOB,
∴
=
,
∴OB=
,
∴S△OAB=
(0<t<2).
∴∠AOB=45°,
∴CD=OD=DE=EF=t,
∴tan∠FOB=
| t |
| 2t |
| 1 |
| 2 |
(2)∵CF∥OB,
∴△ACF∽△AOB,
∴
2
| ||||
2
|
| t |
| OB |
∴OB=
| 2t |
| 2-t |
∴S△OAB=
| 2t |
| 2-t |
点评:此题主要考查了正方形的性质以及相似三角形的判定和性质,题目的综合性较强,难度中等.

练习册系列答案
相关题目
下列每组数据分别表示三根木棒的长度,将它们首尾连接后,不能摆成三角形的一组是( )
| A、3,4,8 |
| B、5,8,11 |
| C、4,4,7 |
| D、8,8,15 |
(-3)100×(-3)-101等于( )
| A、-3 | ||
| B、3 | ||
C、
| ||
D、-
|
 如图,在直角坐标系中,矩形ABCD的顶点,A的坐标为(1,0),对角线的交点P的坐标为(
如图,在直角坐标系中,矩形ABCD的顶点,A的坐标为(1,0),对角线的交点P的坐标为(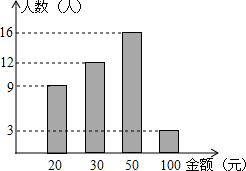 春节将至,某中学八年级(1)班共有40名同学参加了“春节送温暖”捐款活动.活动结束后,生活委员小林将捐款情况进行了统计,并绘制成如右的统计图.
春节将至,某中学八年级(1)班共有40名同学参加了“春节送温暖”捐款活动.活动结束后,生活委员小林将捐款情况进行了统计,并绘制成如右的统计图.