Question

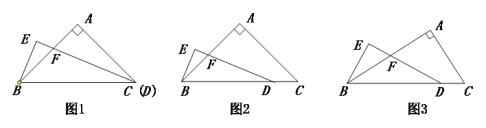
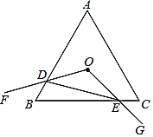
【题目】如图，等边三角形的边长为8，点是的内心，，绕点旋转，分别交线段、于、两点，连接，给出下列四个结论：①点也一定是的外心；②；③四边形的面积始终等于；④周长的最小值为6．上述结论中正确的个数是（ ）

A.1B.2C.3D.4

Answer 1

【答案】B

【解析】

连接OB、OC，如图，利用等边三角形的性质得∠ABO=∠OBC=∠OCB=30°，再证明∠BOD=∠COE，于是可判断△BOD≌△COE，所以BD=CE，OD=OE，则可对① 进行判断；利用S△BOD=S△COE得到四边形ODBE的面积=S△ABC=，则可对③进行判断；作OH⊥DE，如图，则DH=EH，计算出S△ODE=OE2，利用S△ODE随OE的变化而变化和四边形ODBE的面积为定值可对②进行判断；由于△BDE的周长=BC+DE=4+DE=4+OE，根据垂线段最短，当OE⊥BC时，OE最小，△BDE的周长最小，计算出此时OE的长则可对④进行判断．

连接OB、OC，如图，

∵△ABC为等边三角形，

∴∠ABC=∠ACB=60，

∵点O是等边△ABC的内心，

∴OB=OC，OB、OC分别平分∠ABC和∠ACB，

∴∠ABO=∠OBC=∠OCB=30，

∴∠BOC=120，即∠BOE+∠COE=120，

而∠DOE=120，即∠BOE+∠BOD=120，

∴∠BOD=∠COE，

在△BOD和△COE中，

，

∴△BOD≌△COE，

∴BD=CE，OD=OE，所以①正确；

∴S△BOD=S△COE，

∴四边形ODBE的面积=S△OBC=S△ABC=，所以③错误；

作OH⊥DE，如图，则DH=EH，

∵∠DOE=120，

∴∠ODE=∠OEH=30，

∴OH=OE，HE=OH=OE，

∴DE=OE，

∴S△ODE=.OEOE=，

即S△ODE 随OE的变化而变化，

而四边形ODBE的面积为定值，

∴S△ODE≠S△BDE；所以②错误；

∵BD=CE，

∴△BDE的周长=BD+BE+DE=CE+BE+DE=BC+DE=4+DE=4+OE，

当OE⊥BC时，OE最小，△BDE的周长最小，此时OE=，

∴△BDE周长的最小值=4+2=6，所以④正确.

故选：B.