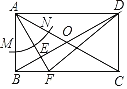
题目内容
【题目】在△ABC中,∠A=90°,点D在线段BC上,∠EDB=![]() ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
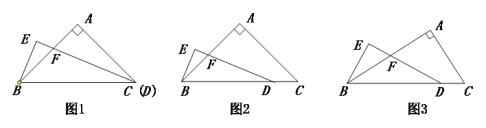
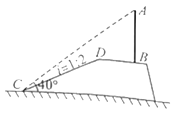
探究:当AB=AC且C,D两点重合时(如图1)探究:
(1)线段BE与FD之间的数量关系,直接写出结果 ;
(2)∠EBF= .
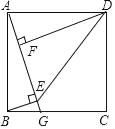
证明:当AB=AC且C,D不重合时,探究线段BE与FD的数量关系,并加以证明.
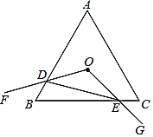
计算:当AB=![]() AC时,如图,求
AC时,如图,求![]() 的值 (用含
的值 (用含![]() 的式子表示).
的式子表示).
【答案】(1)BE=![]() FD;(2)22.5°,证明:BE=
FD;(2)22.5°,证明:BE=![]() FD,见解析;计算:
FD,见解析;计算:![]()
【解析】
探究:(1)首先延长CA与BE交于点G,根据∠EDB=![]() ∠C,BE⊥DE,判断出BE=EG=
∠C,BE⊥DE,判断出BE=EG=![]() BG;然后根据全等三角形的判定方法,判断出△ABG≌△ACF,即可判断出BG=CF=FD,再根据BE=
BG;然后根据全等三角形的判定方法,判断出△ABG≌△ACF,即可判断出BG=CF=FD,再根据BE=![]() BG,可得BE=
BG,可得BE=![]() FD,据此判断即可;
FD,据此判断即可;
(2)根据(1)的结论易求得答案;
证明:过点D作DG∥CA,与BE的延长线相交于点G,与AB相交于点H,仿照(1)的方法判断出△DEB≌△DEG和△GBH≌△FDH,即可推出结论;
计算:利用(2)的结论证得△GBH∽△FDH和△BHD∽△BAC,利用对应边成比例即可求得结论.
探究:(1)如图①,延长CA与BE交于点G,

∵∠EDB=![]() ∠C,
∠C,
∴∠EDB =∠EDG,
即CE是∠BCG的平分线,
又∵BE⊥DE,
∴BE=EG=![]() BG,
BG,
∵∠BED=∠BAD=90°,∠BFE=∠CFA,
∴∠EBF=∠ACF,
即∠ABG=∠ACF,
在△ABG和△ACF中,
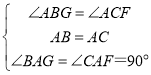 ,
,
∴△ABG≌△ACF,
∴BG=CF=FD,
又∵BE=![]() BG,
BG,
∴BE=![]() FD;
FD;
(2)∵AB=AC,∠A=90°,
∴∠ACB=45![]() ,
,
由(1)得CE是∠BCG的平分线,且∠EBF=∠ACF,
∴∠EBF=![]() ∠ACB=
∠ACB=![]() ;
;
证明:结论BE=![]() FD.
FD.
证明如下:
如图②,过点D作DG∥CA,与BE的延长线相交于点G,与AB相交于点H,

则∠GDB=∠C,∠BHD=∠A=90°=∠GHB.
∵∠EDB=![]() ∠C=
∠C=![]() ∠GDB=∠EDG,
∠GDB=∠EDG,
在△DEB和△DEG中,
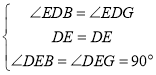 ,
,
∴△DEB≌△DEG,
∴BE=GE=![]() GB.
GB.
∵∠A=90°,AB=AC,
∴∠ABC=∠C=∠GDB,
∴HB=HD.
∵∠BED=∠BHD=90°, ∠BFE=∠DFH,
∴∠EBF=∠HDF,
在△GBH和△FDH中,
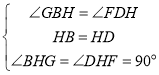 ,
,
∴△GBH≌△FDH,
∴GB=FD,
∴BE=![]() FD;
FD;
计算:∵△DEB≌△DEG,BE=![]() GB,∠BHD=∠BEF=90°,∠EBF=∠HDF,
GB,∠BHD=∠BEF=90°,∠EBF=∠HDF,
∴△GBH∽△FDH,
∴![]() ,即
,即![]() .
.
又∵DG∥CA,
∴△BHD∽△BAC,
∴![]() ,即
,即![]() .
.
∴![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案