题目内容
11.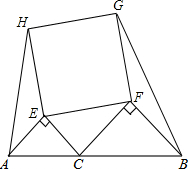 如图,点C在线段AB上,分别以AC和CB为斜边向上作等腰直角△AEC和△CFB,已知这两个等腰直角三角形的直角边分别为6cm和8cm,又以EF为边向上作正方形EFGH,连接AH,BG,则四边形ABGH的面积为222cm2.
如图,点C在线段AB上,分别以AC和CB为斜边向上作等腰直角△AEC和△CFB,已知这两个等腰直角三角形的直角边分别为6cm和8cm,又以EF为边向上作正方形EFGH,连接AH,BG,则四边形ABGH的面积为222cm2.
分析 延长AE,BF,延长线相交于点O,过H作HM⊥AO,过G作GN⊥BO,再证明△HEM≌△GFN≌△EFO≌△EFC后,利用三角形面积公式解答即可.
解答 解:延长AE,BF,延长线相交于点O,过H作HM⊥AO,过G作GN⊥BO,如图: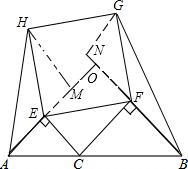
∵∠CEM=90°,∠CFN=90°,∠ECF=90°,
∴∠OEF+∠FEC=∠CFE+∠FEC=90°,∠OFE+∠CFE=∠CFE+∠FEC=90°,
∴∠OEF+∠EFO=90°,
在△OEF和△CFE中,
$\left\{\begin{array}{l}{∠OEF=∠EFC}\\{EF=FE}\\{∠OFE=∠FEC}\end{array}\right.$,
∴△OEF≌△CFE(ASA),
同理可得:△HEM≌△EFC,
△GFN≌△EFC,
∴△HEM≌△GFN≌△EFO≌△EFC,
∴HM=FC=8,GN=CE=6,
∴EF=$\sqrt{{6}^{2}+{8}^{2}}=10$,
∴四边形ABGH的面积=$\frac{1}{2}×6×8+\frac{1}{2}×6×8+\frac{1}{2}×6×6+\frac{1}{2}×8×8+\frac{1}{2}×6×8+10×10$=222cm2.
故答案为:222
点评 此题考查全等三角形的判定和性质,关键是构建全等三角形,再利用面积公式解答.

练习册系列答案
相关题目
1.已知点A(1,0)、B(0,-1)、C(-1,2)、D(2,-1)、E(4、2)中有三个点在关于x的二次函数y=a(x-1)2+k(a>0)的图象上,请结合你学过的抛物线的知识挑选你认为正确的三个点( )
| A. | A、C、E | B. | B、C、D | C. | B、C、E | D. | A、B、D |
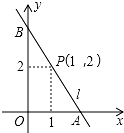 如图,直线l经过点P(1,2),与坐标轴交于A(a,0),B(0,b)两点(其中a<b,如果a+b=6,那么tan∠ABO的值为$\frac{1}{2}$.
如图,直线l经过点P(1,2),与坐标轴交于A(a,0),B(0,b)两点(其中a<b,如果a+b=6,那么tan∠ABO的值为$\frac{1}{2}$.
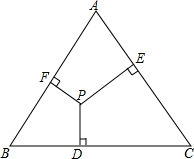 有一块等边三角形的空地,小明和小亮想在这块空地上找到一点,使得这一点到三边的距离之和最短,他们做了几次实验,发现无论三角形内的哪一点到三边的距离之和都是相等的.于是他们编了一道几何题:如图,已知点P为正△ABC内一点,点P到BC,CA,AB的距离分别为PD,PE,PF,试说明PD+PE+PF总是一个定值.这个定值与什么有关?你发现这个事实了吗?你能解出他们编的数学问题吗?
有一块等边三角形的空地,小明和小亮想在这块空地上找到一点,使得这一点到三边的距离之和最短,他们做了几次实验,发现无论三角形内的哪一点到三边的距离之和都是相等的.于是他们编了一道几何题:如图,已知点P为正△ABC内一点,点P到BC,CA,AB的距离分别为PD,PE,PF,试说明PD+PE+PF总是一个定值.这个定值与什么有关?你发现这个事实了吗?你能解出他们编的数学问题吗?