题目内容
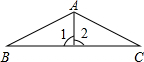 在括号里加注理由.已知:△ABC中,AB=AC,BD=DC,B、D、C在同一条直线上.
在括号里加注理由.已知:△ABC中,AB=AC,BD=DC,B、D、C在同一条直线上.求证:AD⊥BC.
证明:在△ABD和△ACD中
|
∴∠1=∠2(
∵B、D、C在同一直线上(已知)
∴∠BDC=180°(
∴∠1=
| 1 |
| 2 |
∴AD⊥BC(
分析:要证AD⊥BC,则要证明∠1=∠2,则要证明△ABC≌△ACD,由已知条件,易得全等.
解答:证明:在△ABD和△ACD中
,
∴△ABC≌△ACD(SSS).
∴∠1=∠2(全等三角形对应角相等).
∵B、D、C在同一直线上(已知),
∴∠BDC=180°(平角定义).
∴∠1=
∠BDC=90°.
∴AD⊥BC(垂直定义).
|
∴△ABC≌△ACD(SSS).
∴∠1=∠2(全等三角形对应角相等).
∵B、D、C在同一直线上(已知),
∴∠BDC=180°(平角定义).
∴∠1=
| 1 |
| 2 |
∴AD⊥BC(垂直定义).
点评:本题考查三角形全等的判定及性质;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.要根据已知条件在图形上的位置进行选择方法.

练习册系列答案
相关题目
 在括号里加注理由.
在括号里加注理由. 在括号里加注理由.
在括号里加注理由. 在括号里加注理由.已知:△ABC中,AB=AC,BD=DC,B、D、C在同一条直线上.
在括号里加注理由.已知:△ABC中,AB=AC,BD=DC,B、D、C在同一条直线上.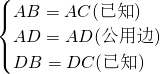 ∴△ABC≌△ACD(________)
∴△ABC≌△ACD(________) ∠BDC=90°
∠BDC=90°
