Question

如图，⊙O的半径为4cm，直线l与⊙O相交于A、B两点，AB=4

3

cm，P为直线l上一动点，以1cm为半径的⊙P与⊙O没有公共点，设PO=dcm，则d的范围是

 

．

Answer 1

考点：圆与圆的位置关系

专题：

分析：根据两圆内切和外切时，求出两圆圆心距，进而得出d的取值范围．

解答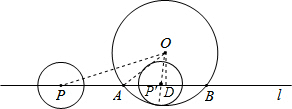：解：连接OP、OA，
∵⊙O的半径为4cm，1cm为半径的⊙P，⊙P与⊙O没有公共点，
∴d＞5时，两圆外离，
当两圆内切时，过点O作OD⊥AB于点D，
OP′=4-1=3cm，OD=

42-(2 3 )2

=2（cm），
∴以1cm为半径的⊙P与⊙O没有公共点时，2≤d＜3，
故答案为：2cm≤d＜3cm或d＞5cm．

点评：此题主要考查了圆与圆的位置关系，根据图形进行分类讨论得出是解题关键．