题目内容
2.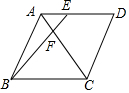 如图,在菱形ABCD中,AB=12,点E为AD上一点,BE交AC于点F,若$\frac{AF}{FC}$=$\frac{1}{3}$,则AE的长为( )
如图,在菱形ABCD中,AB=12,点E为AD上一点,BE交AC于点F,若$\frac{AF}{FC}$=$\frac{1}{3}$,则AE的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 先证明△AFE∽△BCF,然后利用相似三角形的性质即可求出AE的长度.
解答 解:由于AD∥BC,
∴△AEF∽△BCF,
∴$\frac{AF}{FC}=\frac{AE}{BC}$=$\frac{1}{3}$,
∵AB=BC=12,
∴AE=4,
故选(B)
点评 本题考查相似三角形的性质与判定,解题的关键是熟练运用相似三角形的性质,本题属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17. 如图,△ABC为等边三角形,要在△ABC外部取一点D,使得△ABC和△DBC全等,下面是两名同学做法:( )
如图,△ABC为等边三角形,要在△ABC外部取一点D,使得△ABC和△DBC全等,下面是两名同学做法:( )
甲:①作∠A的角平分线l;
②以B为圆心,BC长为半径画弧,交l于点D,点D即为所求;
乙:①过点B作平行于AC的直线l;
②过点C作平行于AB的直线m,交l于点D,点D即为所求.
 如图,△ABC为等边三角形,要在△ABC外部取一点D,使得△ABC和△DBC全等,下面是两名同学做法:( )
如图,△ABC为等边三角形,要在△ABC外部取一点D,使得△ABC和△DBC全等,下面是两名同学做法:( )甲:①作∠A的角平分线l;
②以B为圆心,BC长为半径画弧,交l于点D,点D即为所求;
乙:①过点B作平行于AC的直线l;
②过点C作平行于AB的直线m,交l于点D,点D即为所求.
| A. | 两人都正确 | B. | 两人都错误 | C. | 甲正确,乙错误 | D. | 甲错误,乙正确 |
12.点P(-1,2)关于y轴的对称点为( )
| A. | (1,2) | B. | (-1,-2) | C. | (2,-1) | D. | (1,-2) |
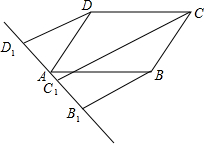 如图,直线l过?ABCD的顶点A,点D1、C1、B1都在直线l上,且DD1∥CC1∥BB1,求证:CC1=DD1+BB1.
如图,直线l过?ABCD的顶点A,点D1、C1、B1都在直线l上,且DD1∥CC1∥BB1,求证:CC1=DD1+BB1. 解不等式组$\left\{\begin{array}{l}{5x-2≥3(x-1)}\\{\frac{1}{2}x-1<5-\frac{3}{2}x}\end{array}\right.$,并把解集在所给数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{5x-2≥3(x-1)}\\{\frac{1}{2}x-1<5-\frac{3}{2}x}\end{array}\right.$,并把解集在所给数轴上表示出来.