题目内容
如图,PA、PB分别切⊙O于A、B,圆周角 AMB=
AMB= ,EF切⊙O于C,交PA、PB于E、F,
,EF切⊙O于C,交PA、PB于E、F, PEF的外心在PE上,PA=3.则AE的长为( )
PEF的外心在PE上,PA=3.则AE的长为( )

A. B.
B.  C. 1 D.
C. 1 D.
B
【解析】
试题分析:连接OA,OB,
∵PA,PB分别切⊙O于A、B,
∴OA⊥PA,OB⊥PB,PA=PB=3,
∵∠AMB=60°,
∴∠AOB=2∠AMB=120°,
∴∠P=180°﹣∠AOB=60°,
∵EF切⊙O于C,
∴EA=EC,FC=FB,
∴△PEF的周长=PE+EF+PF=PE+EC+FC+PF=PE+AE+BF+PF=PA+PB=6,
∵△PEF的外心在PE上,
∴PE是△PEF的外接圆的直径,
∴∠PFE=90°,
设PF=x,则PE=2x,EF= x,
x,
∴x+2x+ x=6,
x=6,
解得:x=3﹣ ,
,
∴PE=6﹣2 ,
,
∴AE=PA﹣PE=3﹣(6﹣2 )=2
)=2 ﹣3.
﹣3.
故选D.

考点: 切线的性质

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,如果∠CAE>∠BAD,那么下列说法中一定正确的是( )
如图,如果∠CAE>∠BAD,那么下列说法中一定正确的是( )| A、∠BAC>∠CAD | B、∠DAE>∠CAD | C、∠CAE<∠BAC+∠DAE | D、∠BAC<∠DAE |
 的一元二次方程方程
的一元二次方程方程 有两个不相等的实数根.
有两个不相等的实数根. 的取值范围;
的取值范围; 取最大整数时,不解方程直接写出方程的两根之和与两根之积.
取最大整数时,不解方程直接写出方程的两根之和与两根之积. ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
 )B(0,4)把
)B(0,4)把 按如图标记的方式连续做旋转变换,这样得到的第2015个三角形中,O点的对应点的坐标为___________.
按如图标记的方式连续做旋转变换,这样得到的第2015个三角形中,O点的对应点的坐标为___________.
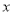 的一元二次方程
的一元二次方程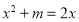 ,没有实数根,则实数
,没有实数根,则实数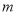 的取值范围是( )
的取值范围是( )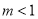 B.
B. 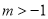 C.
C.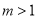 D.
D.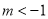
 向左平移1个单位,再向上平移3个单位得到的抛物线,其表达式为( )
向左平移1个单位,再向上平移3个单位得到的抛物线,其表达式为( ) B.
B.
 D.
D.