Question

（14分）把两个全等的等腰直角三角形ABC和EFG（其直角边长均为4）叠放在一起（如图①），且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合．现将三角板EFG绕O点逆时针旋转（旋转角α满足条件：0°＜α＜90°），四边形CHGK是旋转过程中两三角板的重叠部分（如图②）．

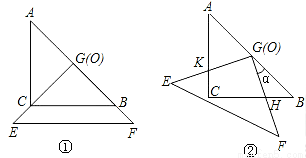
（1）在上述旋转过程中，BH与CK有怎样的数量关系？四边形CHGK的面积有何变化？证明你发现的结论；（要有辅助线哟！）

（2）连接HK，在上述旋转过程中，设BH=x，△GKH的面积为y，求y与x之间的函数关系式，并写出自变量x的取值范围；

（3）在（2）的前提下，是否存在某一位置，使△GKH的面积恰好等于△ABC面积的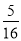，若存在，求出此时x值；若不存在，说明理由。

Answer 1

（1）BH=CK；四边形CHGK的面积不变；（2）y=-2x+4（0＜x＜4）；（3）x=1或x=3．

【解析】

试题分析：（1）连接CG，根据中线的性质得出CG=BG，CG⊥AB，根据旋转图形的性质得出△BGH和△CGK全等，将四边形的面积转化成△CHG的面积+△CGK的面积，根据全等得出△CHG的面积+△BGH的面积，即△ABC面积的一半；（2）连接HK，则BK=CK=x，CH=4－x，根据△GHK的面积=四边形CHGK的面积-△CHK的面积求出函数关系式；（3）根据（2）中的结论列出一元二次方程，然后求出x的值．

试题解析：（1）在上述旋转过程中，BH=CK，四边形CHGK的面积不变。

证明：连接CG，

∵△ABC为等腰直角三角形，O（G）为其斜边中点，∴CG=BG，CG⊥AB，

∴∠ACG=∠B=45°，∵∠BGH与∠CGK均为旋转角，∴∠BGH=∠CGK，

在△BGH与△CGK中，∠B=∠KCG,BG=CG, ∠BCG=∠CGK

∴△BGH≌△CGK（ASA）， ∴BH=CK，△BGH的面积=△CGK的面积．

∴四边形CHGK的面积=△CHG的面积+△CGK的面积=的面积△CHG+△BGH的面积=S△ABC=××4×4=4

即：四边形CHGK的面积为4，是一个定值，在旋转过程中没有变化；

（2）∵AC=BC=4，BK=x，∴CH=4-x，CK=x，连接HK．

由△GHK的面积=四边形CHGK的面积-△CHK的面积，得y=4-x（4-x）=-2x+4 由0°＜α＜90°，得到BH最大=BC=4，∴0＜x＜4；

（3）存在．根据题意，得-2x+4=×8 解这个方程，得=1，=3，

即：当x=1或x=3时，△GHK的面积均等于△ABC的面积的。

考点：图形的旋转、一元二次方程的应用．

考点分析： 考点1：图形的平移与旋转 定义：
将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移。平移是图形变换的一种基本形式。平移不改变图形的形状和大小，平移可以不是水平的。 平移基本性质：
经过平移，对应线段平行（或共线）且相等，对应角相等，对应点所连接的线段平行且相等；
平移变换不改变图形的形状、大小和方向(平移前后的两个图形是全等形)。
（1）图形平移前后的形状和大小没有变化，只是位置发生变化;
（2）图形平移后，对应点连成的线段平行（或在同一直线上）且相等
（3）多次连续平移相当于一次平移。
（4）偶数次对称后的图形等于平移后的图形。
（5）平移是由方向和距离决定的。
这种将图形上的所有点都按照某个方向作相同距离的位置移动，叫做图形的平移运动，简称为平移
平移的条件：确定一个平移运动的条件是平移的方向和距离。 平移的三个要点
1 原来的图形的形状和大小和平移后的图形是全等的。
2 平移的方向。（东南西北，上下左右,东偏南n度，东偏北n度，西偏南n度，西偏北n度）
3 平移的距离。（长度，如7厘米，8毫米等） 平移作用：
1.通过简单的平移可以构造精美的图形。也就是花边，通常用于装饰，过程就是复制-平移-粘贴。
2.平移长于平行线有关,平移可以将一个角,一条线段,一个图形平移到另一个位置,是分散的条件集中到一个图形上,使问题得到解决。 平移作图的步骤：
（1）找出能表示图形的关键点；
（2）确定平移的方向和距离；
（3）按平移的方向和距离确定关键点平移后的对应点；
（4）按原图的顺序，连结各对应点。 试题属性

• 题型：
• 难度：
• 考核：
• 年级：