题目内容
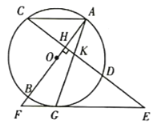
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 的平分线交圆
的平分线交圆![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 是
是![]() 中点,
中点,![]() ,
,![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,点
,点![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)详见解析;(2)详见解析;(3)![]() 的半径长为8
的半径长为8
【解析】
(1)连接OD,见详解图,通过![]() 的平分线交圆
的平分线交圆![]() 于点
于点![]() 和OD=OA及
和OD=OA及![]() ,易证∠ODE为90°;
,易证∠ODE为90°;
(2)根据FG⊥AO,AD平分∠BAC及∠ADE=90°,易证∠AHF=∠HDG,进而可得∠DHG=∠HDG,即可得出结论;
(3)由![]() 可设
可设![]() ,
,![]() ,则
,则![]() ,因为F为OA中点,所以AF=
,因为F为OA中点,所以AF=![]() ,过G做GM⊥AD,易证
,过G做GM⊥AD,易证![]() ,可得
,可得![]() ,
,![]() ,进而
,进而![]() ,即得答案.
,即得答案.
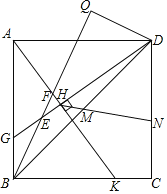
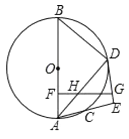
(1)证明:如图①中,![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线;
的切线;
(2)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)∵![]()
设![]() ,
,![]() ,则
,则![]()
∵点![]() 是
是![]() 中点,
中点,
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]() ,
,![]()
![]()
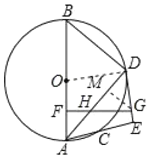
由(2)可知,![]()
过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]() ,
,
∴在![]() 中,
中,![]()
![]()
∴![]()
∴![]()
∴![]() 的半径长为8
的半径长为8

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目