Question

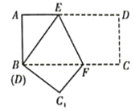
【题目】如图，将矩形纸片折叠，使点与点重合，点落在处，折痕为，若，，则线段的长度为________．

Answer 1

【答案】

【解析】

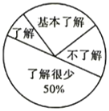
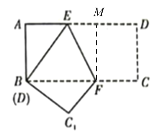
先过点F作FM⊥AD于M，利用勾股定理可求出BE，再利用翻折变换的知识，可得到BE=DE，∠BEF=∠DEF，再利用平行线可得∠BEF=∠BFE，故有BE=BF．求出EM，再次使用勾股定理可求出EF的长．

解：过点F作FM⊥AD于M，

∵EF是折痕，
∴BE=DE，∠BEF=∠DEF，
又∵AD∥BC，
∴∠BFE=∠DEF，
∴∠BEF=∠BFE，
∴BE=BF，
在Rt△ABE中，设AE=x，AB=4，BE=DE=8-x，

则有x2+42=（8-x）2解得x=3，则BE=5，
在Rt△FEM中，EM=AM-AE=BF-AE=BE-AE=5-3=2，FM=4，

∴EF=，

故答案为：.