题目内容
如图，扇形AOB的圆心角为直角，正方形OCDE内接于扇形，点C、E、D分别在OA、OB、AB上，过点A作AF⊥ED交ED的延长线于F，垂足为F．如果正方形的边长OC为1，那么阴影部分的面积为
- A.
-1 - B.2
- C.3
- D.+1
A
分析：根据题意可得出两个矩形全等，则阴影部分的面积等于等于矩形ACDF的面积．
解答：易得两个矩形全等，
∵OC=1，∴由勾股定理得OA=，
∴S阴影=S矩形=（-1）×1=-1，
故选A．
点评：本题考查了扇形面积的计算，正方形的性质以及勾股定理，是基础知识比较简单．
分析：根据题意可得出两个矩形全等，则阴影部分的面积等于等于矩形ACDF的面积．
解答：易得两个矩形全等，
∵OC=1，∴由勾股定理得OA=
，∴S阴影=S矩形=（
-1）×1=-1，故选A．
点评：本题考查了扇形面积的计算，正方形的性质以及勾股定理，是基础知识比较简单．
练习册系列答案
考前必练系列答案
相关题目
如图，扇形OAB的半径OA=r，圆心角∠AOB=90°，点C是
（2012•珠海三模）如图：扇形OAB的圆心角∠AOB=120°，半径OA=6cm，
（1997•台湾）已知：如图，扇形AOB．求作：一个与OA、OB、
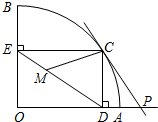
如图，扇形OAB的半径OA=r，圆心角∠AOB=90°，点C是
上异于A、B的动点，过点C作CD⊥OA于点D，作CE⊥OB于点E，点M在DE上，DM=2EM，过点C的直线CP交OA的延长线于点P，且∠CPO=∠CDE．
r；