题目内容
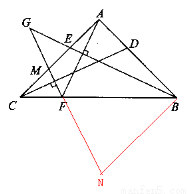
(12分)如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M。

(1)求证:△ADC≌△AEB ,
(2)判断△EGM是什么三角形,并证明你的结论;
(3)猜想线段BG、AF与FG的数量关系并证明你的结论。
(1)详见解析;(2)△EGM是等腰三角形,证明详见解析;(3)BG=AF+FG;证明详见解析
【解析】
试题分析:(1)∵等腰直角三角形ABC中,∠BAC=90°,
∴AC=AB,∠ACB=∠ABC=45°,
在△ADC和△AEB中
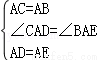
∴△ADC≌△AEB(SAS),
(2)△EGM为等腰三角形;
理由:∵△ADC≌△AEB,
∴∠1=∠3,
∵∠BAC=90°,
∴∠3+∠2=90°,∠1+∠4=90°,
∴∠4+∠3=90°
∵FG⊥CD,
∴∠CMF+∠4=90°,
∴∠3=∠CMF,
∴∠GEM=∠GME,
∴EG=MG,△EGM为等腰三角形.
(3)线段BG、AF与FG的数量关系为BG=AF+FG.
理由:如图所示:过点B作AB的垂线,交GF的延长线于点N,
∵BN⊥AB,∠ABC=45°,
∴∠FBN=45°=∠FBA.
∵FG⊥CD,
∴∠BFN=∠CFM=90°﹣∠DCB,
∵AF⊥BE,
∴∠BFA=90°﹣∠EBC,∠5+∠2=90°,
由(1)可得∠DCB=∠EBC,
∴∠BFN=∠BFA,
在△BFN和△BFA中
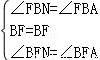
∴△BFN≌△BFA(ASA),
∴NF=AF,∠N=∠5,
又∵∠GBN+∠2=90°,
∴∠GBN=∠5=∠N,
∴BG=NG,
又∵NG=NF+FG,
∴BG=AF+FG.
考点:特殊三角形的综合运用

练习册系列答案
相关题目
 ,π,
,π, ,0.121121112…,
,0.121121112…, 中,有理数有( )个.
中,有理数有( )个. 的一元二次方程
的一元二次方程 的一个根是0,则
的一个根是0,则 的值为 .
的值为 .


