Question

3．如图，将矩形纸片ABCD折叠，使点A与点C重合，折痕为EF，若AB=4，BC=2，求线段EF的长．

Answer 1

分析 如图，AC交EF于点O，由勾股定理先求出AC的长度，根据折叠的性质可判断出RT△EOC～RT△ABC，从而利用相似三角形的对应边成比例可求出OE，再由EF=2OE可得出EF的长度．

解答 解：如图所示，AC交EF于点O，
由勾股定理知AC=2$\sqrt{5}$，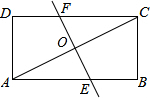
又∵折叠矩形使C与A重合时有EF⊥AC，
则Rt△AOE∽Rt△ABC，
∴$\frac{OE}{BC}$=$\frac{AO}{AB}$，
∴OE=$\frac{\sqrt{5}}{2}$，
故EF=2OE=$\sqrt{5}$．
故答案为：$\sqrt{5}$．

点评 本题考查了翻折变换、勾股定理及矩形的性质，难度一般，解答本题的关键是判断出Rt△AOE∽Rt△ABC，利用相似三角形的性质得出OE的长．