题目内容
11．
彤彤将一些半径相同的小圆按如图所示的规律摆放，第①个图形由2个小圆构成，第②个图形由6个小圆构成，第③个图形由12个小圆构成，…，依此规律，当完成第⑧个图形时，一共所需要的小圆的个数是（ ）| A． | 72 | B． | 168 | C． | 230 | D． | 240 |
分析 由题意可知：第一个图形中有1×2=2个小圆，第二个图形中有2×3=6个小圆，第三个图形中有3×4=12个小圆，第四个图形中有4×5=20个小圆，…第n个图形有n（n+1）=（n2+n）个小圆，由此代入求得答案即可．
解答 解：第一个图形中有1×2=2个小圆，
第二个图形中有2×3=6个小圆，
第三个图形中有3×4=12个小圆，
第四个图形中有4×5=20个小圆，
…
第n个图形有n（n+1）=（n2+n）个小圆，
所以完成第⑧个图形时，一共所需要的小圆的个数是8×9=72．
故选：A．
点评 此题主要考查了图形的变化规律，通过归纳与总结结合图形得出图形个数之间的规律是解决问题的关键，注意公式必须符合所有的图形．
练习册系列答案
名校课堂系列答案
相关题目
6．意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两个数的和．现以这组数中的各个数作为边长构造如下正方形：
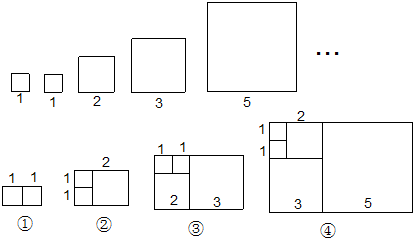
再分别依次从左到右取2个、3个、4个、5个正方形拼成矩形并记为①、②、③、④．相应矩形的周长如表所示：
若按此规律继续作矩形，则序号为⑥的矩形周长是68．
再分别依次从左到右取2个、3个、4个、5个正方形拼成矩形并记为①、②、③、④．相应矩形的周长如表所示：
| 序号 | ① | ② | ③ | ④ |
| 周长 | 6 | 10 | 16 | 26 |
如图，OP平分∠BOA，∠BOA=45°，PC∥OA，PD⊥OA，若PC=4，则PD等于2$\sqrt{2}$．
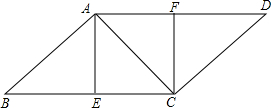如图，在?ABCD中，OA=OC，E，F分别是边BC，AD的中点．