题目内容
14. 如图,在?ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为30°.
如图,在?ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为30°.
分析 由平行四边形的性质得出∠ABC=∠D=100°,AB∥CD,得出∠BAD=180°-∠D=80°,由等腰三角形的性质和三角形内角和定理求出∠ABE=70°,即可得出∠EBC的度数.
解答 解:∵四边形ABCD是平行四边形,
∴∠ABC=∠D=100°,AB∥CD,
∴∠BAD=180°-∠D=80°,
∵AE平分∠DAB,
∴∠BAE=80°÷2=40°,
∵AE=AB,
∴∠ABE=(180°-40°)÷2=70°,
∴∠EBC=∠ABC-∠ABE=30°;
故答案为:30°.
点评 此题主要考查了平行四边形的性质,等腰三角形的性质,三角形和内角和定理等知识;关键是掌握平行四边形对边平行,对角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
则这些运动员成绩的中位数、众数分别为( )
| 成绩/m | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 2 | 3 | 2 | 3 | 4 | 1 |
| A. | 1.65、1.70 | B. | 1.65、1.75 | C. | 1.70、1.75 | D. | 1.70、1.70 |
19.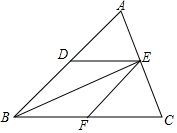 如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
 如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )| A. | AB=AC | B. | AD=BD | C. | BE⊥AC | D. | BE平分∠ABC |
6.下列计算正确的是( )
| A. | 2x+3y=5xy | B. | (m+3)2=m2+9 | C. | (xy2)3=xy6 | D. | a10÷a5=a5 |
 下面是课本中“作一个角等于已知角”的尺规作图过程.
下面是课本中“作一个角等于已知角”的尺规作图过程.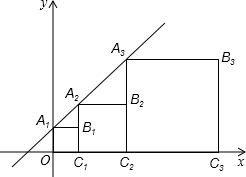 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3和C1,C2,C3,…分别在直线y=x+1和x轴上,则点
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3和C1,C2,C3,…分别在直线y=x+1和x轴上,则点