题目内容
 如图,在平面直角坐标系中,点C(-3,0),直线y=-
如图,在平面直角坐标系中,点C(-3,0),直线y=-| 3 |
| 3 |
(1)求点A,点B的坐标;
(2)若点P从C点出发,以每秒1个单位的速度沿线段CB运动,连接AP,设△ABP的面积为S,点P的运动时间为t秒,求S与t的函数式;
(3)在(2)条件下,是否存在点P,使以点A,B,P为顶点的三角形与△AOB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)根据函数自变量为零时,可得函数图象与y轴的交点,根据函数值为零时,可得函数图象与x轴的交点;
(2)根据勾股定理,可得 AB、BC的长,根据勾股定理逆定理,可得∠ABC的度数,根据线段的和差,可得BP的长,根据三角形的面积公式,可得答案;
(3)分类讨论:△AOB∽△ABP,△AOB∽△PBA,根据相似三角形的性质,可得BP的长,根据线段的和差,可得BP的长.
(2)根据勾股定理,可得 AB、BC的长,根据勾股定理逆定理,可得∠ABC的度数,根据线段的和差,可得BP的长,根据三角形的面积公式,可得答案;
(3)分类讨论:△AOB∽△ABP,△AOB∽△PBA,根据相似三角形的性质,可得BP的长,根据线段的和差,可得BP的长.
解答:解:(1)当y=0时,-
x+
=0解得x=1,即A点坐标是(1,0),
当x=0时,y=
,即B点坐标是(0,
);
(2)由勾股定理得,AB=
=
=2,
BC=
=
=2
.
由勾股定理的逆定理,得
AB2+CB2=22+(2
)2=16,AC2=[1-(-3)]2=16,
AB2+BC2=AC2,
△ABC是直角三角形,∠ABC是直角.
CP=t,当P在线段BC上时,BP=BC-CP=2
-t,当P在线段BC的延长线上时,BP=t-2
;
由直角三角形的面积公式,得S=
BP•AB,即
S=
;
(3)存在点P,使以点A,B,P为顶点的三角形与△AOB相似,
如图:
 ,
,
当△AOB∽△ABP时,
=
,解得BP=2
,P1(-3,0),P3(3,2
);
当△AOB∽△PBA时,
=
,解得BP=
,PC=
,由特殊角三角函数值,得P2(-1,
),P4(1,
).
| 3 |
| 3 |
当x=0时,y=
| 3 |
| 3 |
(2)由勾股定理得,AB=
| OB2+OA2 |
(
|
BC=
| OB2+OC2 |
(
|
| 3 |
由勾股定理的逆定理,得
AB2+CB2=22+(2
| 3 |
AB2+BC2=AC2,
△ABC是直角三角形,∠ABC是直角.
CP=t,当P在线段BC上时,BP=BC-CP=2
| 3 |
| 3 |
由直角三角形的面积公式,得S=
| 1 |
| 2 |
S=
|
(3)存在点P,使以点A,B,P为顶点的三角形与△AOB相似,
如图:
 ,
,当△AOB∽△ABP时,
| AO |
| AB |
| BO |
| BP |
| 3 |
| 3 |
当△AOB∽△PBA时,
| AO |
| BP |
| BO |
| AB |
2
| ||
| 3 |
| 4 |
| 3 |
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
点评:本题考查了一次函数的综合题,利用了函数值与自变量的关系,勾股定理及逆定理,相似三角形的性质.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
若多项式4x2-12xy+ky2是完全平方式,则k的值是( )
| A、3 | B、6 | C、9 | D、36 |
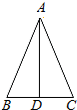 如图,△ABC中,AB=AC,D为BC的中点,以下结论:
如图,△ABC中,AB=AC,D为BC的中点,以下结论:(1)△ABD≌△ACD;
(2)AD⊥BC;
(3)∠B=∠C;
(4)AD是△ABC的角平分线.
其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在△ABC中,AB=AC=BD,且D为BC上一点,CD=AD,则∠B的度数为( )
如图,在△ABC中,AB=AC=BD,且D为BC上一点,CD=AD,则∠B的度数为( )| A、30° | B、36° |
| C、40° | D、45° |
-
的系数是( )
| 2πx3y |
| 5 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
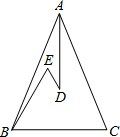 如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=4cm,DE=3cm,则BC=
如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=4cm,DE=3cm,则BC=