Question

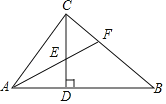
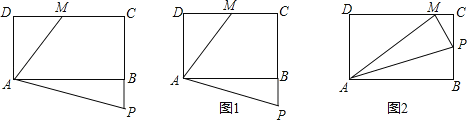
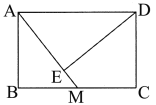
【题目】如图，矩形ABCD中，AB=4，BC=6，M是BC的中点，DEAM，E为垂足．

（1）证明：△ABM∽△DEA；

（2）求△ADE的面积．

Answer 1

【答案】（1）见解析；（2）.

【解析】

（1）先根据矩形的性质，得到AD∥BC，则∠DAE=∠AMB，又由∠DEA=∠B，根据有两角对应相等的两三角形相似，即可证明出△DAE∽△AMB；（2）由△DAE∽△AMB，根据相似三角形的对应边成比例，即可求出DE、AE的长，进而可求面积．

（1）证明：∵四边形ABCD是矩形，

∴AD∥BC，

∴∠DAE=∠AMB，

又∵∠DEA=∠B=90°，

∴△DAE∽△AMB；

（2）由（1）知△DAE∽△AMB，

∴DE：AD=AB：AM，

∵M是边BC的中点，BC=6，

∴BM=3，

又∵AB=4，∠B=90°，

∴AM=5，

∴，

∴ ，，

∴ △ADE的面积为．