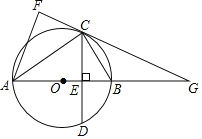
题目内容
【题目】如图,在![]() 中,弦
中,弦![]() 垂直于直径
垂直于直径![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,将
,将![]() 沿
沿![]() 翻转得到
翻转得到![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 为
为![]() 的中点,①求证:四边形
的中点,①求证:四边形![]() 是菱形;②若
是菱形;②若![]() ,求
,求![]() 的半径长.
的半径长.
【答案】(1)见解析;(2)①见解析,②4
【解析】
(1)连接OC,由OA=OC得∠OAC=∠OCA,结合折叠的性质得∠OCA=∠FAC,于是可判断OC∥AF,然后根据切线的性质得直线FC与⊙O相切;
(2)①连接OD、BD,利用直角三角形斜边上的中线的性质可证得CB=OC=OD=BD,再根据菱形的判定定理即可判定;
②首先证明△OBC是等边三角形,在Rt△OCE中,根据![]() ,构建方程即可解决问题;
,构建方程即可解决问题;
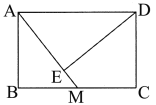
(1)如图,连接OC,
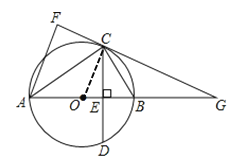
∵OA=OC,
∴∠OAC=∠OCA,
由翻折的性质,有∠OAC=∠FAC,∠AEC=∠AFC=90°,
∴∠FAC=∠OCA,
∴![]() ∥AF,
∥AF,
∴∠OCG=∠AFC=90°,
故FG是⊙O的切线;
(2)①如图,连接OD、BD,
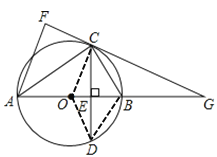
∵CD垂直于直径AB,
∴OC=OD,BC=BD,
又∵B为OG的中点,
∴![]() ,
,
∴CB=OB,
又∵OB=OC,
∴CB=OC,
则有CB=OC=OD=BD,
故四边形OCBD是菱形;
②由①知,△OBC是等边三角形,
∵CD垂直于直径AB,
∴![]() ,
,
∴![]() ,
,
设⊙O的半径长为R,
在Rt△OCE中,
有![]() ,即
,即![]() ,
,
解之得:![]() ,
,
⊙O的半径长为:4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目