题目内容
1. 如图,AB和⊙O切于点B,AB=5,OB=3,则tanA=$\frac{3}{5}$.
如图,AB和⊙O切于点B,AB=5,OB=3,则tanA=$\frac{3}{5}$.
分析 由于直线AB与⊙O相切于点B,则∠OBA=90°,AB=5,OB=3,根据三角函数定义即可求出tanA.
解答 解:∵直线AB与⊙O相切于点B,
则∠OBA=90°.
∵AB=5,OB=3,
∴tanA=$\frac{OB}{AB}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题主要考查了利用切线的性质和锐角三角函数的概念解直角三角形的问题.

练习册系列答案
相关题目
16.某工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料全部生产A、B两种产品共50件,生产A、B两种产品与所需原料情况如下表所示:
(1)该工厂生产A、B两种产品有哪几种方案?
(2)若生成一件A产品可获利80元,生产一件B产品可获利120元,怎样安排生产可获得最大利润?
| 原料 型号 | 甲种原料(千克) | 乙种原料(千克) |
| A产品(每件) | 9 | 3 |
| B产品(每件) | 4 | 10 |
(2)若生成一件A产品可获利80元,生产一件B产品可获利120元,怎样安排生产可获得最大利润?
13. 如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
 如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )| A. | 由小到大 | B. | 由大到小 | ||
| C. | 不变 | D. | 先由小到大,后由大到小 |
10.下面角的图示中,能与30°角互补的是( )
| A. |  | B. |  | C. |  | D. |  |
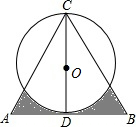 如图,△ABC是边长为4的等边三角形,D为AB边的中点,以CD为直径画圆,则图中阴影部分的面积为2.5$\sqrt{3}$-π(结果保留π).
如图,△ABC是边长为4的等边三角形,D为AB边的中点,以CD为直径画圆,则图中阴影部分的面积为2.5$\sqrt{3}$-π(结果保留π). 平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1-∠2=24°.
平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1-∠2=24°.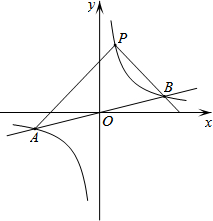 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方. 4月26日,2015黄河口(东营)国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200$\sqrt{3}$+200米.
4月26日,2015黄河口(东营)国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200$\sqrt{3}$+200米.