Question

【题目】如图，已知AD是等腰△ABC底边BC上的高，sinB= ，点E在AC上，且AE：EC=2：3，则tan∠ADE=（ ）
A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：如图．作EF∥CD交AD于F点．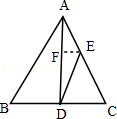
∵sinB=sinC= = ，
∴设AD=4x，则AC=5x，CD=3x，
∵ = = ，
∴FD= x，AF= x．
∵ = = ，
∴EF= x．
∴tan∠ADE= = ，
故选：B．
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识，掌握等腰三角形的两个底角相等（简称：等边对等角），以及对解直角三角形的理解，了解解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．