题目内容
已知x-y=6,xy=-8,
(1)求x2+y2的值;
(2)求代数式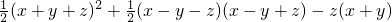 的值.
的值.
解:(1)∵x-y=6,xy=-8,
∴(x-y)2=x2+y2-2xy,
∴x2+y2=(x-y)2+2xy=36-16=20;
(2)∵ (x+y+z)2+
(x+y+z)2+ (x-y-z)(x-y+z)-z(x+y),
(x-y-z)(x-y+z)-z(x+y),
= (x2+y2+z2+2xy+2xz+2yz)+
(x2+y2+z2+2xy+2xz+2yz)+ [(x-y)2-z2]-xz-yz,
[(x-y)2-z2]-xz-yz,
= x2+
x2+ y2+
y2+ z2+xy+xz+yz+
z2+xy+xz+yz+ x2+
x2+ y2-xy-
y2-xy- z2-xz-yz,
z2-xz-yz,
=x2+y2,
又∵x2+y2=20,
∴原式=20.
分析:(1)由(x-y)2=x2+y2-2xy,即可得x2+y2=(x-y)2+2xy,将x-y=6,xy=-8代入即可求得x2+y2的值;
(2)首先化简 (x+y+z)2+
(x+y+z)2+ (x-y-z)(x-y+z)-z(x+y),可得
(x-y-z)(x-y+z)-z(x+y),可得 (x+y+z)2+
(x+y+z)2+ (x-y-z)(x-y+z)-z(x+y)=x2+y2,由(1)即可求得答案.
(x-y-z)(x-y+z)-z(x+y)=x2+y2,由(1)即可求得答案.
点评:此题考查了完全平方公式的应用.注意熟记公式的几个变形公式对解题大有帮助.
∴(x-y)2=x2+y2-2xy,
∴x2+y2=(x-y)2+2xy=36-16=20;
(2)∵
 (x+y+z)2+
(x+y+z)2+ (x-y-z)(x-y+z)-z(x+y),
(x-y-z)(x-y+z)-z(x+y),=
 (x2+y2+z2+2xy+2xz+2yz)+
(x2+y2+z2+2xy+2xz+2yz)+ [(x-y)2-z2]-xz-yz,
[(x-y)2-z2]-xz-yz,=
 x2+
x2+ y2+
y2+ z2+xy+xz+yz+
z2+xy+xz+yz+ x2+
x2+ y2-xy-
y2-xy- z2-xz-yz,
z2-xz-yz,=x2+y2,
又∵x2+y2=20,
∴原式=20.
分析:(1)由(x-y)2=x2+y2-2xy,即可得x2+y2=(x-y)2+2xy,将x-y=6,xy=-8代入即可求得x2+y2的值;
(2)首先化简
 (x+y+z)2+
(x+y+z)2+ (x-y-z)(x-y+z)-z(x+y),可得
(x-y-z)(x-y+z)-z(x+y),可得 (x+y+z)2+
(x+y+z)2+ (x-y-z)(x-y+z)-z(x+y)=x2+y2,由(1)即可求得答案.
(x-y-z)(x-y+z)-z(x+y)=x2+y2,由(1)即可求得答案.点评:此题考查了完全平方公式的应用.注意熟记公式的几个变形公式对解题大有帮助.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知3x=4y,则
=( )
| x |
| y |
A、
| ||
B、
| ||
C、-
| ||
D、-
|