题目内容
如图，在正三角形ABC的边BC，CA上分别有点E、F，且满足BE=CF=a，EC=FA=b （a＞b ）．当BF平分AE时，则
的值为
- A.
- B.
- C.
- D.
C
分析：过E作AC的平行线，则△HOE∽△FOA，得出HE=AF=b，再由
=
，代入化简即可．
解答：
解：过E作AC的平行线与BF相交于点H，
则△HOE∽△FOA，又BF平分AE，即HE=AF=b，
在△BCF中，=，即
=
，
a2=b（a+b），化简得a=b，
即=．
故选C．
点评：本题主要考查了平行线分线段成比例的性质问题，能够熟练运用其性质求解一些简单的计算问题．
分析：过E作AC的平行线，则△HOE∽△FOA，得出HE=AF=b，再由
=，代入化简即可．解答：
解：过E作AC的平行线与BF相交于点H，则△HOE∽△FOA，又BF平分AE，即HE=AF=b，
在△BCF中，
=，即=，a2=b（a+b），化简得a=
b，即
=．故选C．
点评：本题主要考查了平行线分线段成比例的性质问题，能够熟练运用其性质求解一些简单的计算问题．
练习册系列答案
相关题目
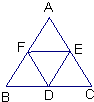
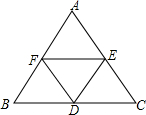如图，在正三角形ABC中，D、E、F分别为BC、CA、AB的中点，请你数一数，有
12、如图，在正三角形ABC中，点D，E分别AB，AC在上，且DE∥BC，如果BC=12cm，AD：DB=1：3，那么三角形ADE的周长=
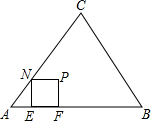已知△ABC是正三角形，正方形EFPN的顶点E、F在边AB上，顶点N在边AC上．