题目内容
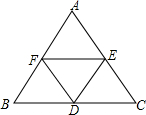 如图,在正三角形ABC中,D、E、F分别为BC、CA、AB的中点,请你数一数,有
如图,在正三角形ABC中,D、E、F分别为BC、CA、AB的中点,请你数一数,有分析:根据三角形的中位线定理求出DE∥AB,DE=
AB,AF=BF=
AB,推出DE=AF,DE∥AF,根据平行四边形的判定即可推出答案;根据D、E、F分别为BC、CA、AB的中点和正三角形的性质推出AE=BD,根据等腰梯形的判定即可推出答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵D、E、F分别为BC、CA、AB的中点,
∴DE∥AB,DE=
AB,AF=BF=
AB,
∴DE=AF,DE∥AF,
∴四边形AFED是平行四边形,
同理:四边形EFBD、EFDC是平行四边形,
∵E是AC的中点,D是BC的中点,
∴AE=
AC,BD=
BC,
∵三角形ABC是等边三角形,
∴AC=BC,
∴AE=BD,
∵DE∥AB,
∴四边形AEDB是等腰梯形,
同理:四边形BFEC、DFAC是等腰梯形,
故答案为:3,3.
∴DE∥AB,DE=
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=AF,DE∥AF,
∴四边形AFED是平行四边形,
同理:四边形EFBD、EFDC是平行四边形,
∵E是AC的中点,D是BC的中点,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∵三角形ABC是等边三角形,
∴AC=BC,
∴AE=BD,
∵DE∥AB,
∴四边形AEDB是等腰梯形,
同理:四边形BFEC、DFAC是等腰梯形,
故答案为:3,3.
点评:本题主要考查对等腰梯形的判定,平行四边形的判定,等边三角形的性质,三角形的中位线等知识点的理解和掌握,能综合运用性质进行推理是解此题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
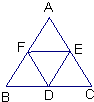
 12、如图,在正三角形ABC中,点D,E分别AB,AC在上,且DE∥BC,如果BC=12cm,AD:DB=1:3,那么三角形ADE的周长=
12、如图,在正三角形ABC中,点D,E分别AB,AC在上,且DE∥BC,如果BC=12cm,AD:DB=1:3,那么三角形ADE的周长=
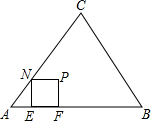 已知△ABC是正三角形,正方形EFPN的顶点E、F在边AB上,顶点N在边AC上.
已知△ABC是正三角形,正方形EFPN的顶点E、F在边AB上,顶点N在边AC上.