题目内容
若sinα+cosα=p,则以sinα和cosα为两根的一元二次方程是
- A.x2-px=0
- B.2x2-2px+p2-1=0
- C.2x2-2px-p2+1=0
- D.2x2-2px+p2=0
B
分析:要求以sinα和cosα为两根的一元二次方程,关键先求出sinαcosα,然后根据根与系数的关系即可解答.
解答:∵sinα+cosα=p,两边平方,
得sin2α+cos2α+2sinα•cosα=p2,
∴1+2sinα•cosα=p2,
∴sinα•cosα= ,
,
故所求方程为: =0,
=0,
即2x2-2px+p2-1=0.
故选B.
点评:本题考查了根与系数的关系及同角三角函数的关系,属于基础题,关键是熟记x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q,反过来可得p=-(x1+x2),q=x1x2.
分析:要求以sinα和cosα为两根的一元二次方程,关键先求出sinαcosα,然后根据根与系数的关系即可解答.
解答:∵sinα+cosα=p,两边平方,
得sin2α+cos2α+2sinα•cosα=p2,
∴1+2sinα•cosα=p2,
∴sinα•cosα=
 ,
,故所求方程为:
 =0,
=0,即2x2-2px+p2-1=0.
故选B.
点评:本题考查了根与系数的关系及同角三角函数的关系,属于基础题,关键是熟记x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q,反过来可得p=-(x1+x2),q=x1x2.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
若sinα+cosα=p,则以sinα和cosα为两根的一元二次方程是( )
| A、x2-px=0 | B、2x2-2px+p2-1=0 | C、2x2-2px-p2+1=0 | D、2x2-2px+p2=0 |
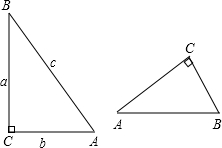 角A的正弦,余弦存在关系式sin2A+cos2A=1试说明.
角A的正弦,余弦存在关系式sin2A+cos2A=1试说明.