题目内容
若sinα+cosα=m,则sinα-cosα(0°<α<45°)=
-
| 2-m2 |
-
.| 2-m2 |
分析:首先求出2sinα•cosα=m2-1,进而得出(sinα-cosα)2=2-m2,即可得出sinα-cosα的值.
解答:解:∵sinα+cosα=m,
∴(sinα+cosα)2=m2,
∴sin2α+cos2α+2sinα•cosα=m2,
∴1+2sinα•cosα=m2,
∴2sinα•cosα=m2-1,
∴(sinα-cosα)2=sin2α+cos2α-2sinα•cosα=1-(m2-1)=2-m2,
∵0°<α<45°,
∴sinα<cosα,
∴sinα-cosα=-
.
故答案为:-
.
∴(sinα+cosα)2=m2,
∴sin2α+cos2α+2sinα•cosα=m2,
∴1+2sinα•cosα=m2,
∴2sinα•cosα=m2-1,
∴(sinα-cosα)2=sin2α+cos2α-2sinα•cosα=1-(m2-1)=2-m2,
∵0°<α<45°,
∴sinα<cosα,
∴sinα-cosα=-
| 2-m2 |
故答案为:-
| 2-m2 |
点评:此题主要考查了同角的三角函数以及完全平方公式的应用,关键是掌握同一锐角的正弦与余弦之间的关系:对任一锐角α,都有sin2α+cos2α=1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若sinα+cosα=p,则以sinα和cosα为两根的一元二次方程是( )
| A、x2-px=0 | B、2x2-2px+p2-1=0 | C、2x2-2px-p2+1=0 | D、2x2-2px+p2=0 |
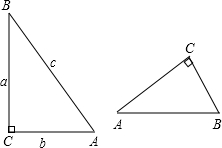 角A的正弦,余弦存在关系式sin2A+cos2A=1试说明.
角A的正弦,余弦存在关系式sin2A+cos2A=1试说明.