题目内容
20. 如图所示,甲、乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字.游戏规定:转动两个转盘停止后,指针所指的两个数字之积为奇数时,甲获胜;为偶数时,乙获胜.
如图所示,甲、乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字.游戏规定:转动两个转盘停止后,指针所指的两个数字之积为奇数时,甲获胜;为偶数时,乙获胜.(1)求转动B转盘,指针指到偶数的概率;
(2)你认为这个游戏规则对双方公平吗?请简要说明理由.
分析 (1)由题意可知其中的偶数只有6一个数,利用概率公式计算即可;
(2)游戏是否公平,关键要看是否游戏双方赢的机会相等,本题中即两转盘上的数字之积为偶数或奇数时的概率是否相等,求出概率比较,即可得出结论.
解答 解:(1)P(指针指到偶数)=$\frac{1}{3}$;
(2)根据题意,画出树状图如下:
| AB积 | 1 | 2 | 3 | (列出表格或画出树状图得3分) 4 |
| 5 | 奇 | 偶 | 奇 | 偶 |
| 6 | 偶 | 偶 | 偶 | 偶 |
| 7 | 奇 | 偶 | 奇 | 偶 |
∴P(甲胜)=$\frac{1}{3}$,P(乙胜)=$\frac{2}{3}$,
∵P(甲胜)≠P(乙胜)
∴这个游戏规则不公平.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
10. 如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8$\sqrt{3}$m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的髙度是( )m.
如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8$\sqrt{3}$m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的髙度是( )m.
 如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8$\sqrt{3}$m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的髙度是( )m.
如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8$\sqrt{3}$m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的髙度是( )m.| A. | 8$\sqrt{6}$+24 | B. | 8$\sqrt{6}$+8 | C. | 24+8$\sqrt{3}$ | D. | 8+8$\sqrt{3}$ |
15.若(m-2)${x}^{{m}^{2}-2}$-x+1=0是一元二次方程,则m的值为( )
| A. | ±2 | B. | 2 | C. | -2 | D. | 以上结论都不对 |
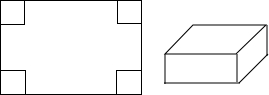 如图是以长为120cm,宽为80cm的长方形硬纸,在它的四个角处各剪去一个边长为20cm的正方形后,将其折叠成如图所示的无盖的长方体,则这个长方体的体积为64000立方厘米.
如图是以长为120cm,宽为80cm的长方形硬纸,在它的四个角处各剪去一个边长为20cm的正方形后,将其折叠成如图所示的无盖的长方体,则这个长方体的体积为64000立方厘米.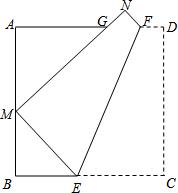 如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明:
如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明: