Question

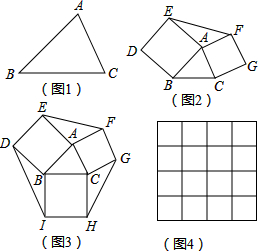
7．在图1中，△ABC的顶点都在网格线的交点上，由此我们称这种三角形为格点三角形．
（1）在图1中，每个小正方形的边长为1时，AC=$\sqrt{13}$；
（2）在图2中，若每个小正方形的边长为a，请在此网格上画出三边长分别为$\sqrt{5}$a、2$\sqrt{2}$a、$\sqrt{17}$a的格点三角形；
（3）图3是由12个长为m，宽为n小矩形构成的网格，请在此网格中画出边长分别为$\sqrt{{m}^{2}+16{n}^{2}}$、$\sqrt{9{m}^{2}+4{n}^{2}}$、2$\sqrt{{m}^{2}+{n}^{2}}$的格点三角形．

Answer 1

分析 （1）直接利用勾股定理得出AC的长；
（2）根据勾股定理画出长为$\sqrt{5}$a、2$\sqrt{2}$a、$\sqrt{17}$a的三角形即可．
（3）根据勾股定理画出长为$\sqrt{{m}^{2}+16{n}^{2}}$、$\sqrt{9{m}^{2}+4{n}^{2}}$、2$\sqrt{{m}^{2}+{n}^{2}}$的三角形即可．

解答 解：（1）AC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$；
故答案为：$\sqrt{13}$；

（2）如图2所示：△ABC就是所求的三角形．其中AB=$\sqrt{5}$a、AC=2$\sqrt{2}$a、BC=$\sqrt{17}$a．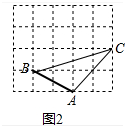


（3）如图3所示：△ABC就是所求的三角形．其中AB=$\sqrt{{m}^{2}+16{n}^{2}}$、BC=$\sqrt{9{m}^{2}+4{n}^{2}}$、AC=2$\sqrt{{m}^{2}+{n}^{2}}$．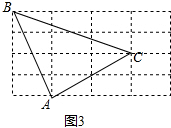

点评 本题考查勾股定理、作图设计应用等知识，解题的关键是灵活应用勾股定理解决问题，体现了数形结合的思想，属于中考常考题型．