题目内容
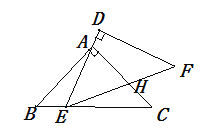
如图,△ABC和△DEF是两个全等的等腰直角三角形,其中∠BAC=∠EDF=90°、AB=AC=1,△DEF中的点E在BC边上运动(不与B、C重合),DE始终经过点A,设EF交AC于点H
(1)求证:△ABE∽△ECH;
(2)设BE= 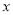 ,CH=
,CH= 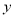 ,求
,求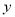 与
与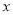 的函数关系式,并求当
的函数关系式,并求当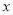 取何值时,
取何值时, 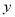 有最大值,最大值是多少?
有最大值,最大值是多少?
(3)当点E运动到何处时,△ABE是等腰三角形,并求出此时CH的长。
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
题目内容
如图,△ABC和△DEF是两个全等的等腰直角三角形,其中∠BAC=∠EDF=90°、AB=AC=1,△DEF中的点E在BC边上运动(不与B、C重合),DE始终经过点A,设EF交AC于点H
(1)求证:△ABE∽△ECH;
(2)设BE= 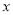 ,CH=
,CH= 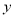 ,求
,求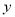 与
与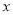 的函数关系式,并求当
的函数关系式,并求当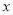 取何值时,
取何值时, 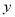 有最大值,最大值是多少?
有最大值,最大值是多少?
(3)当点E运动到何处时,△ABE是等腰三角形,并求出此时CH的长。

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案