题目内容
9．
如图，射线OC平分∠AOB，点P在OC上，且PD⊥OA于点D，PE⊥OB于点E，若OD=8，OP=10，则PE的长为6．
分析 根据勾股定理求出PD，根据角平分线性质得出PE=PD，即可得出答案．
解答 解：∵PD⊥OA，
∴∠PDO=90°，
在Rt△PDO中，由勾股定理得：PD=$\sqrt{O{P}^{2}-O{D}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6，
∵射线OC平分∠AOB，点P在OC上，且PD⊥OA于点D，PE⊥OB于点E，
∴PE=PD=6，
故答案为：6．
点评 本题考查了勾股定理和角平分线性质，能灵活运用角平分线性质进行推理是解此题的关键．
练习册系列答案
核心素养学练评系列答案
相关题目
如图所示，已知∠1=∠2，AB=AD，要使△ABC≌△ADE，还需条件∠B=∠D或∠C=∠E或AC=AE．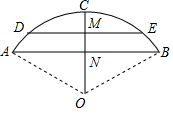
一跨河桥，桥拱是圆弧形，跨度（AB）为12米，拱高（CN）为2米，
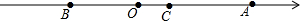如图，在数轴上原点O表示的数是0，B点表示的数是m，A表示的数是n，且（m+4）2+|n-8|=0．