��Ŀ����
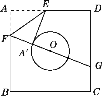
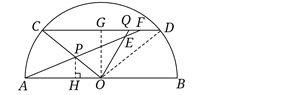
����Ŀ����֪����ͼ��AB�ǰ�ԲO��ֱ������CD��AB������P��Q�ֱ����߶�OC��CD�ϣ���DQ��OP��AP���ӳ���������OQ�ཻ�ڵ�E������CD�ཻ�ڵ�F(��F���C��D���غ�)��AB��20��cos ��AOC��![]() .��OP��x����CPF�����Ϊy.
.��OP��x����CPF�����Ϊy.
(1)��֤��AP��OQ��
(2)��y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
(3)����OPE��ֱ��������ʱ�����߶�OP�ij���
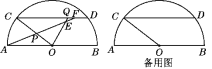
���𰸡���1�������������2��y��![]() ��x��ȡֵ��ΧΪ
��x��ȡֵ��ΧΪ![]() <x<10����3���߶�OP�ij�Ϊ8.
<x<10����3���߶�OP�ij�Ϊ8.
��������
��1������OD��������ֱ��ƽ�У��ڴ�����Ⱥ͵ȱ߶ԵȽǵ����ʿɵó���AOC����ODC�������ñ߽DZߵ��ж϶�����֤����AOP�ա�ODQ������ȫ�������ζ�Ӧ����ȼ���֤��AP��OQ.
��2������P��PH��OA�ڵ�H������O��OG��CD�ڵ�G.������ֱ��ƽ�У��ڴ�����ȿ�֤����PFC�ס�PAO���������Ǻ����ļ��㹫ʽ���ɶ�������x��ʾ����PAO��������������������������֮�ȵ������Ʊȵ�ƽ��������x��ʾ��y���ֱ�ȡ��F���D�͵�C�غ�ʱ�����ô������������������ε����ʿ����x��ֵ����Ϊ��F���C��D���غϣ����ɵó�X��ȡֵ��Χ��
��3�����������֪������POEΪֱ��������ʱ���ɷ�����������ۣ�����POE=90�㡢��OPE=90�㡢��OEP=90�����ֱ������������OP�ij�����ȡ���ϣ�2����x��ȡֵ��Χ�Ľ����
(1)֤��������OD��
��OC��OD��
���OCD����ODC.
��CD��AB�����AOC����OCD��
���AOC����ODC.
����AOP����ODQ��
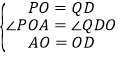
���AOP�ա�ODQ��
��AP��OQ.
(2)��PH��OA������ΪH����OG��CD������ΪG.
��cos��AOC=![]() �ɵ�OH��
�ɵ�OH��![]() x��
x��
��RT��OPH�У��ɹ��ɶ����ɵã�PH=![]() ��
��
��S��AOP��![]() =3x.
=3x.
��CD��AB��
���PFC�ס�PAO��
��![]() ��
��
��![]() =
=![]() .
.
����F���C�غ�ʱ��OP��10.
����F���D�غ�ʱ��
��cos��OCG��![]() ��cos��AOC��
��cos��AOC��![]() ��
��
��CG��8��
��CD��16.
��![]() ��
��
��![]()
���x��![]() .
.
������F���C��D���غϣ�
��x��ȡֵ��ΧΪ![]() <x<10.
<x<10.
(3)�⣺����POE��90��ʱ��CQ��![]() ��OP��DQ��CD��CQ��3.5(��ȥ)��
��OP��DQ��CD��CQ��3.5(��ȥ)��
����OPE��90��ʱ������APO��90�㣬
��OP��AO��cos��COA��8��
����OEP��90��ʱ��������������ڣ�
���߶�OP�ij�Ϊ8.

 ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�