题目内容
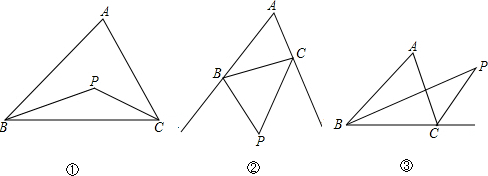
17.如图所示.在△ABC中.∠A=70°.(1)在图①中.点P是△ABC的两内角平分线的交点.求∠P的度数;
(2)在图②中,点P是△ABC的两外角平分线的交点.求∠P的度数;
(3)在图③中.点P是△ABC的一内角和一外角平分线的交点.求∠P的度数;
(4)当∠A=α时.以上三种情形你能分别写出∠P的度数吗?(直接写出即可)
分析 (1)根据三角形内角和定理求出∠ABC+∠ACB的度数,再根据BP、CP分别平分∠ABC与∠ACB求出∠PBC+∠PCB的度数,由三角形内角和定理即可得出∠P的度数;
(2)先根据外角平分线的性质求出∠PBC、∠PCB与∠A的关系,再由三角形内角和定理解答即可;
(3)根据角平分线的定义可得∠CBP=$\frac{1}{2}$∠ABC,根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义表示出∠PCE,然后整理即可得到∠BPC=$\frac{1}{2}$∠A,代入数据计算即可得解;
(4)根据(1)(2)(3)的方法即可得到结论.
解答 解:(1)∵BP、CP分别是∠ABC、∠ACB的角平分线,
∴∠PBC=$\frac{1}{2}$∠ABC,∠PCB=$\frac{1}{2}$∠ACB,
∴∠P=180°-(∠PBC+∠PCB)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A=125°;
(2)∵BP、CP是∠ABC和∠ACB外角的平分线,
∴∠CBP=$\frac{1}{2}$(∠A+∠ACB),∠BCP=$\frac{1}{2}$(∠A+∠ABC),
∵∠ABC+∠ACB=180°-∠A,
∠P=180°-∠CBP-∠BCP=180°-$\frac{1}{2}$(∠A+∠ACB+∠A+∠ABC)
=180°-$\frac{1}{2}$(2∠A+180°-∠A)
=90°-$\frac{1}{2}$∠A.
=55°;
(3)如图,∵BP平分∠ABC,
∴∠CBP=$\frac{1}{2}$∠ABC,
∵CP平分△ABC的外角,
∴∠PCE=$\frac{1}{2}$∠ACE=$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC,
在△BCD中,由三角形的外角性质,∠PCE=∠CBP+∠P=$\frac{1}{2}$∠ABC+∠P,
∴$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ABC+∠BPC,
∴∠P=$\frac{1}{2}$∠A=35°;
(4)①∵BP、CP分别是∠ABC、∠ACB的角平分线,
∴∠PBC=$\frac{1}{2}$∠ABC,∠PCB=$\frac{1}{2}$∠ACB,
∴∠P=180°-(∠PBC+∠PCB)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$α;
②∵BP、CP是∠ABC和∠ACB外角的平分线,
∴∠CBP=$\frac{1}{2}$(∠A+∠ACB),∠BCP=$\frac{1}{2}$(∠A+∠ABC),
∵∠ABC+∠ACB=180°-∠A,
∠P=180°-∠CBP-∠BCP=180°-$\frac{1}{2}$(∠A+∠ACB+∠A+∠ABC)
=180°-$\frac{1}{2}$(2∠A+180°-∠A)
=90°-$\frac{1}{2}$α;
③∵BP平分∠ABC,
∴∠CBP=$\frac{1}{2}$∠ABC,
∵CP平分△ABC的外角,
∴∠PCE=$\frac{1}{2}$∠ACE=$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC,
在△BCD中,由三角形的外角性质,∠PCE=∠CBP+∠P=$\frac{1}{2}$∠ABC+∠P,
∴$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ABC+∠BPC,
∴∠P=$\frac{1}{2}$α.
点评 本题考查的是三角形内角和定理以及角平分线的性质,熟知三角形内角和是180°是解答此题的关键.

| 年份 | 1957 | 1974 | 1987 | 1999 | 2010 | 2025 |
| 人口数 | 30亿 | 40亿 | 50亿 | 60亿 | 70亿 | 80亿 |
(2)如果要用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是怎样的?
 一些立体图形可由一些平面图形绕一条直线旋转而得到,这样的几何体叫旋转体,试思考:
一些立体图形可由一些平面图形绕一条直线旋转而得到,这样的几何体叫旋转体,试思考: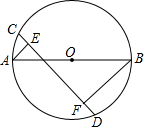 如图,在⊙O中,AB是直径,CD是弦,过点A、B两点分别作CD的垂线,垂足分别是点E、F,AE=1,BF=3,CD=6,求EF的长.
如图,在⊙O中,AB是直径,CD是弦,过点A、B两点分别作CD的垂线,垂足分别是点E、F,AE=1,BF=3,CD=6,求EF的长. 小颖装饰新家,她为自己的房间选择了一款新窗帘,窗帘的上部(帘楣)设计成图中阴影部分所示的图案,小颖想知道挂上帘楣后窗户上还有多少面积可以射进阳光,你能帮她求出来吗?
小颖装饰新家,她为自己的房间选择了一款新窗帘,窗帘的上部(帘楣)设计成图中阴影部分所示的图案,小颖想知道挂上帘楣后窗户上还有多少面积可以射进阳光,你能帮她求出来吗?