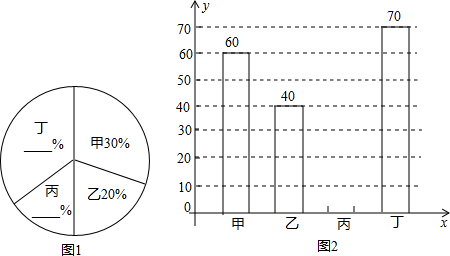
题目内容
1.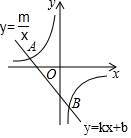 如图,已知A(-4,2),B(n,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,2),B(n,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.(1)求m,n的值;
(2)求一次函数的关系式;
(3)结合图象直接写出一次函数小于反比例函数的x的取值范围.
分析 (1)先把A的坐标代入反比例函数y=$\frac{m}{x}$中求出m的值,写出反比例函数的解析式,再将点B的坐标代入求n的值;
(2)利用待定系数法求一次函数的关系式;
(3)结合图象写结论即可.
解答 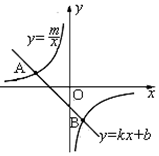 解:(1)把A(-4,2)代入y=$\frac{m}{x}$,即:m=-8,
解:(1)把A(-4,2)代入y=$\frac{m}{x}$,即:m=-8,
∴y=-$\frac{8}{x}$,
把B(n,-4)代入y=-$\frac{8}{x}$得:
解得n=2,
∴B(2,-4);
(2)把A(-4,2),B(2,-4)代入y=kx+b中,
得 $\left\{\begin{array}{l}{2=-4k+b}\\{-4=2k+b}\end{array}\right.$,
解得k=-1,b=-2,
∴y=-x-2;
(3)由图象得:一次函数小于反比例函数的x的取值范围是:-4<x<0或x>2.
点评 本题考查了反比例函数与一次函数的交点问题、利用待定系数法求反比例函数与一次函数的解析式,并利用数形结合得出自变量x的取值范围.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
6.用一副三角尺不能画出来的角的度数是( )
| A. | 75° | B. | 105° | C. | 95° | D. | 150° |
11.有下列各数:0.01,10,-$\frac{1}{3}$,-|-2|,-90,-(-3.5),其中属于负数的共有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,已知△ABC.
如图,已知△ABC.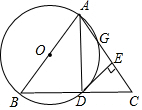 如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连结AD,并过点D作⊙O的切线DE,交AC于点E.求证:
如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连结AD,并过点D作⊙O的切线DE,交AC于点E.求证: