题目内容
已知正三角形的边长为a，其内切圆半径为r，外接圆半径为R，则r：a：R等于________．
1：2
：2
分析：根据等边三角形的三线合一，得其等边三角形的半边、内切圆的半径和外接圆的半径组成了一个30°的直角三角形．即可求解．
解答：等边三角形的半边、内切圆的半径和外接圆的半径组成了一个30°的直角三角形，则r?a?R=1：2：2．
如图：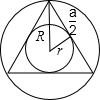
点评：注意：正三角形的内切圆的半径、外接圆的半径和半边组成了一个30°的直角三角形．
：2分析：根据等边三角形的三线合一，得其等边三角形的半边、内切圆的半径和外接圆的半径组成了一个30°的直角三角形．即可求解．
解答：等边三角形的半边、内切圆的半径和外接圆的半径组成了一个30°的直角三角形，则r?a?R=1：2
：2．如图：
点评：注意：正三角形的内切圆的半径、外接圆的半径和半边组成了一个30°的直角三角形．
练习册系列答案
相关题目
已知正三角形的边长为6，则其内切圆的半径为（ ）
A、2
| ||
| B、3 | ||
C、
| ||
| D、1 |
已知正三角形的边长为6，则这个正三角形的外接圆半径是（ ）
A、
| ||
B、2
| ||
| C、3 | ||
D、3
|
已知正三角形的边长为3，则它的外接圆的面积为（ ）
| A、3π | ||||
| B、6π | ||||
| C、9π | ||||
D、
|
如图，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成．已知正三角形的边长为1，则凸轮的周长等于（ ）