题目内容
 如图,正三角形的边长为6,点P为BC边上一点,且PC=4,D为AC上一点,∠APD=60°,则CD的长为
如图,正三角形的边长为6,点P为BC边上一点,且PC=4,D为AC上一点,∠APD=60°,则CD的长为
- A.

- B.

- C.

- D.

C
分析:根据等边三角形性质和三角形的内角和定理求出∠B=∠C,∠CDP=∠APB,证△CDP∽△BPA,得出比例式,代入求出即可.
解答:∵△ABC是等边三角形,
∴BC=AC=BC=6,∠C=∠B=60°,
∴∠CDP+∠CPD=180°-60°=120°,
∵∠APD=60°,
∴∠CPD+∠APB=120°,
∴∠CDP=∠APB,
∵∠C=∠B,
∴△CPD∽△BAP,
∴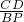 =
=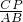 ,
,
∴ =
= ,
,
∴DC= ,
,
故选C.
点评:本题考查了相似三角形的性质和判定,三角形的内角和定理,等边三角形的性质定理等知识点的应用,关键是能推出△CPD∽△BAP.
分析:根据等边三角形性质和三角形的内角和定理求出∠B=∠C,∠CDP=∠APB,证△CDP∽△BPA,得出比例式,代入求出即可.
解答:∵△ABC是等边三角形,
∴BC=AC=BC=6,∠C=∠B=60°,
∴∠CDP+∠CPD=180°-60°=120°,
∵∠APD=60°,
∴∠CPD+∠APB=120°,
∴∠CDP=∠APB,
∵∠C=∠B,
∴△CPD∽△BAP,
∴
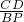 =
=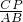 ,
,∴
 =
= ,
,∴DC=
 ,
,故选C.
点评:本题考查了相似三角形的性质和判定,三角形的内角和定理,等边三角形的性质定理等知识点的应用,关键是能推出△CPD∽△BAP.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,正三角形的边长为4,则点C的坐标是( )
如图,正三角形的边长为4,则点C的坐标是( )| A、(4,-2) | ||
| B、(4,2) | ||
C、(2
| ||
D、(-2,2
|
 如图,正三角形的边长为6,点P为BC边上一点,且PC=4,D为AC上一点,∠APD=60°,则CD的长为( )
如图,正三角形的边长为6,点P为BC边上一点,且PC=4,D为AC上一点,∠APD=60°,则CD的长为( )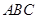 的边长为
的边长为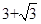 .
. 的顶点
的顶点 在边
在边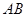 上,顶点
上,顶点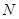 在边
在边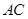 上.在正三角形
上.在正三角形 为位似中心,作正方形
为位似中心,作正方形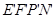 ,且使正方形
,且使正方形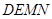 和正方形
和正方形 ,使得
,使得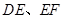 在边
在边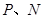 分别在边
分别在边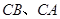 上,求这两个正方形面积和的最大值及最小值,并说明理由.
上,求这两个正方形面积和的最大值及最小值,并说明理由.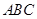 的边长为
的边长为 .
.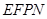 的顶点
的顶点 在边
在边 上,顶点
上,顶点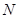 在边
在边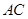 上.在正三角形
上.在正三角形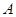 为位似中心,作正方形
为位似中心,作正方形 ,且使正方形
,且使正方形 和正方形
和正方形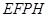 ,使得
,使得 在边
在边 分别在边
分别在边 上,求这两个正方形面积和的最大值及最小值,并说明理由.
上,求这两个正方形面积和的最大值及最小值,并说明理由.