Question

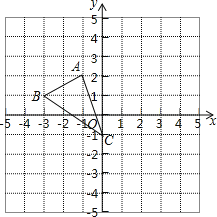
【题目】如图，已知在平面直角坐标系内有A（﹣1，2）、B（﹣3，1）、C（0，﹣1）．

（1）画出△ABC关于O点成中心对称的△A1B1C1，直接写出B1：（　 　，　 　）

（2）将△ABC绕O点顺时针方向旋转90°后得到△A2B2C2，画出旋转后的图形并直接写出B2坐标：（　 　，　 　）

（3）求（2）中线段AB所扫过的面积．

Answer 1

【答案】（1）见解析，3，﹣1；（2）见解析，1，3；（3）

【解析】

（1）根据中心对称的性质画出△A1B1C1，再写出B1的坐标即可；

（2）根据图形旋转的性质画出△A2B2C2，写出B2的坐标即可；

（3）根据勾股定理求出OA，OB的长，再根据线段AB所扫过的面积=-即可得出结论．

（1）如图所示．

故答案为：3，﹣1；

（2）如图所示．

故答案为：1，3；

（3）∵OA=，OB＝，

∴线段AB所扫过的面积＝S扇形BOB2﹣S扇形AOA2＝﹣＝．