题目内容
15.已知平行四边形ABCD的面积为1,K、L、M、N分别是边AB、BC、CD、DA的中点,由AL、AM、BN、BM、CK、CN、DK、DL围成的八边形EGPHFTQR,八边形EGPHFTQR的面积为多少?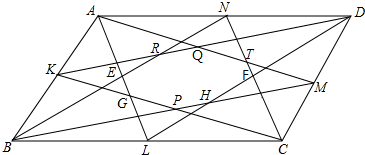
分析 连接AC、BD、KM、NL交于点O,将八边形面积分成8块面积相等的小三角形面积,求出一块,再乘以8即可.
解答 解:如图: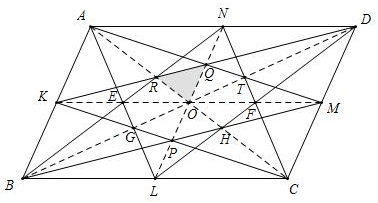
连接AC与BD交点点O,连接KM、NL,
由于K、L、M、N分别为平行四边形ABCD四边的中点,
则A、R、O、H、C共线,B、G、O、T、D共线,K、E、O、F、M共线,N、Q、O、P、L共线,
八边形EGPHFTQR的面积八块小三角形面积,
易知Q为ON中点,
∴${S}_{△ORQ}=\frac{1}{2}{S}_{△ORN}$,
∵R是△ABD的重心,
∴$\frac{AR}{RO}=\frac{2}{1}$,
∴${S}_{△ORN}=\frac{1}{3}{S}_{△OAN}$,
∵${S}_{△OAN}=\frac{1}{8}{S}_{平行四边形ABCD}$,
∴${S}_{△ORN}=\frac{1}{24}{S}_{平行四边形ABCD}$,
∴${S}_{△ORQ}=\frac{1}{48}{S}_{平行四边形ABCD}$,
同理可证剩下7个小三角形的面积也是平行四边形面积的$\frac{1}{48}$,
∴${S}_{八边形EGPHFTQR}=\frac{1}{48}×1×8$=$\frac{1}{6}$.
点评 本题主要考查等积变换,难度适中.对于两个三角形:若高相等,则面积之比等于底之比;若底相同,则面积之比等于高之比;等底等高的两个三角形面积相等.明白这些原理外加三角形重心性质是解决本题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
7.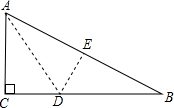 如图一直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图一直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
 如图一直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图一直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )| A. | 2cm | B. | 3cm | C. | 1.5cm | D. | 4cm |
5.最小的正有理数( )
| A. | 是0 | B. | 是1 | C. | 是0.00001 | D. | 不存在 |
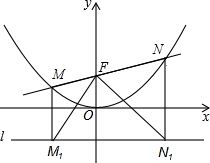 如图,过点F(0,1)的直线y=kx+b与抛物线y=$\frac{1}{4}$x2交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2>0).
如图,过点F(0,1)的直线y=kx+b与抛物线y=$\frac{1}{4}$x2交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2>0).
 若∠B=40°,A、C边上任意两点,∠BAC与∠ACB的平分线交于P1,则∠P1=110°,D、F也边上任意两点,∠BFD与∠FDB的平分线交于P2,…按这样规律,则∠P2015=110°.
若∠B=40°,A、C边上任意两点,∠BAC与∠ACB的平分线交于P1,则∠P1=110°,D、F也边上任意两点,∠BFD与∠FDB的平分线交于P2,…按这样规律,则∠P2015=110°.