题目内容
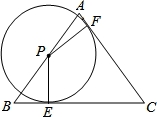
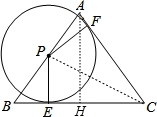
如图,△ABC中AB=AC=5,BC=6,点P在边AB上,以P为圆心的⊙P分别与边AC、BC相切于点E、F,则⊙P的半径PE的长为( )
A.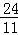 B.2 C.
B.2 C.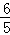 D.
D.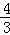
A【考点】切线的性质.
【专题】计算题.
【分析】连结CP,作AH⊥BC于H,如图,设⊙P的半径为r,根据等腰三角形的性质得BH=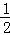 BC=3,则利用勾股定理可计算出AH=4,再根据切线的性质得PE⊥BC,PF⊥AC,利用S△ABC=S△PAC+S△PBC得到
BC=3,则利用勾股定理可计算出AH=4,再根据切线的性质得PE⊥BC,PF⊥AC,利用S△ABC=S△PAC+S△PBC得到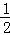 BC×AH=
BC×AH=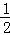 BC×PE+
BC×PE+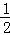 AC×PF,即6×4=6r+5r,然后解方程即可.
AC×PF,即6×4=6r+5r,然后解方程即可.
【解答】解:连结CP,作AH⊥BC于H,如图,设⊙P的半径为r,
∵AB=AC=5,
∴BH=CH=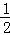 BC=3,
BC=3,
∴AH=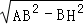 =4,
=4,
∵以P为圆心的⊙P分别与边AC、BC相切于点E、F,
∴PE⊥BC,PF⊥AC,
∵S△ABC=S△PAC+S△PBC,
∴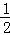 BC×AH=
BC×AH=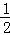 BC×PE+
BC×PE+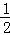 AC×PF,
AC×PF,
即6×4=6r+5r,
∴r=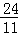 .
.
故选A.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了等腰三角形的性质和三角形面积公式.

练习册系列答案
相关题目
九年级(1)班数学活动选出甲、乙两组各10名学生,进行趣味数学答题比赛,共10题,答对题数统计如表一:
(表一)
| 答对题数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲组 | 1 | 0 | 1 | 5 | 2 | 1 |
| 乙组 | 0 | 0 | 4 | 3 | 2 | 1 |
(表二)
| 平均数 | 众数 | 中位数 | 方差 | |
| 甲组 | 8 | 8 | 8 | 1.6 |
| 乙 | 8 | __________ | __________ | __________ |
(1)根据表一中统计的数据,完成表二;
(2)请你从平均数和方差的角度分析,哪组的成绩更好些?
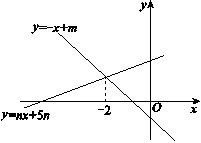
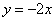 的图象沿
的图象沿 轴向上平移4个单位长度后与y轴交于点B,与x轴交于点C.
轴向上平移4个单位长度后与y轴交于点B,与x轴交于点C.

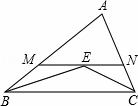
 CB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
CB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )