题目内容
8.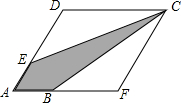 如图,是由梯形ABCD和梯形AECF所组成的,阴影表示的是这两个梯形的重合部分,若这两个梯形完全相同,且AD=CF,AE=$\frac{1}{3}CD$,四边形AFCD的面积为S,则阴影部分的面积为$\frac{1}{3}$s.
如图,是由梯形ABCD和梯形AECF所组成的,阴影表示的是这两个梯形的重合部分,若这两个梯形完全相同,且AD=CF,AE=$\frac{1}{3}CD$,四边形AFCD的面积为S,则阴影部分的面积为$\frac{1}{3}$s.
分析 易证四边形AFCD是菱形,由菱形的性质和全等三角形的判定方法可证明△EDC≌△BFC,进而可得两个三角形的面积相等,易求△DEC和四边形ADCF的面积关系,进而可得到阴影部分的面积和四边形ADCF的数量关系.
解答 解:∵梯形ABCD和梯形AECF完全相同,
∴AD=AF,DC=CF,
∵AD=CF,
∴AD=AF=CF=CD,
∴四边形AFCD是菱形,
∴AD∥CF,∠D=∠F,
∵AE=AB,
∴DE=CF,
在△EDC和△BFC中
$\left\{\begin{array}{l}{DE=FB}\\{∠D=∠F}\\{DC=FC}\end{array}\right.$,
∴△EDC≌△BFC(SAS),
∴两个三角形的面积相等,
∵AE=$\frac{1}{3}CD$,
∴DE=$\frac{2}{3}$AD,
∴S△DEC=$\frac{1}{3}$S四边形ADCF,
∴S阴影=s-$\frac{1}{3}$s-$\frac{1}{3}$s=$\frac{1}{3}$s,
故答案为:$\frac{1}{3}$s.
点评 本题考查了梯形的性质、菱形的判定和性质以及平行四边形的面积公式运用、全等三角形的判定和性质,能够证明四边形ADCF是菱形是解题关键.

练习册系列答案
相关题目
18.下面生活中的物体的运动情况可以看成平移的是(2)(5).
(1)摆动的钟摆;(2)在笔直的公路上行驶的汽车;(3)随风摆动的旗帜;
(4)汽车玻璃上雨刷的运动;(5)从楼顶自由落下的球(球不旋转).
(1)摆动的钟摆;(2)在笔直的公路上行驶的汽车;(3)随风摆动的旗帜;
(4)汽车玻璃上雨刷的运动;(5)从楼顶自由落下的球(球不旋转).
3.下列说法中,正确的是( )
| A. | -1,3,5,-2,2,-1这组数据的方差是7 | |
| B. | 用长分别为2cm,3cm,5cm的线围成三角形是必然事件 | |
| C. | “嫦娥三号”发射前,对其零部件应抽取一部分进行检查 | |
| D. | 茗茗上学经过十字路口遇到红灯时随机事件 |
18.正方形的边长是2,它的对角线长为( )
| A. | 1 | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |