题目内容
4.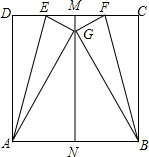 如图,M、N分别是正方形ABCD边DC、AB的中点,分别以AE、BF为折痕,使点D、点C落在MN的点G处,则△ABG是等边三角形.
如图,M、N分别是正方形ABCD边DC、AB的中点,分别以AE、BF为折痕,使点D、点C落在MN的点G处,则△ABG是等边三角形.
分析 由折叠的性质可知AG=AD,BG=BC,然后根据正方形的性质可知:AD=AB=BC,从而可知:AG=AB=BG.
解答 解:由折叠的性质可知AG=AD,BG=BC,
∵四边形ABCD是正方形,
∴AD=AB=BC.
∴AG=AB=BG.
∴△ABG是等边三角形.
故答案为:等边.
点评 本题主要考查的是翻折的性质、等边三角形的判定和正方形的性质,由折叠的性质证得:AG=AD,BG=BC是解题的关键.

练习册系列答案
相关题目
14.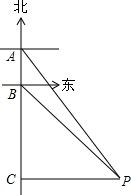 有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )海里.
有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )海里.
 有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )海里.
有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )海里.| A. | 10$\sqrt{3}$ | B. | 10$\sqrt{2}$-10 | C. | 10 | D. | 10$\sqrt{3}$-10 |
 如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
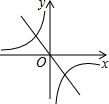
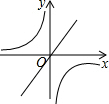
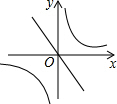
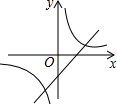
如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.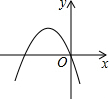 如果二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=$\frac{b}{x}$在同一坐标系中的图象大致是( )
如果二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=$\frac{b}{x}$在同一坐标系中的图象大致是( )