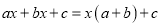题目内容
如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作等腰直角三角形ADE,AD=AE,∠DAE=90º.解答下列问题:
(1) 如果AB=AC,∠BAC=90º.
①当点D在线段BC上时(与点B不重合),如图乙,线段CE、BD之间的位置关系为,数量关系为.(不用证明)
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?



(2) 如果AB≠AC,∠BAC≠90º,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外)?画出相应的图形,并说明理由.
见解析 【解析】试题分析:(1)①根据∠BAD=∠CAE,BA=CA,AD=AE,运用“SAS”证明△ABD≌△ACE,根据全等三角形性质得出对应边相等,对应角相等,即可得到线段CE、BD之间的关系;②先根据“SAS”证明△ABD≌△ACE,再根据全等三角形性质得出对应边相等,对应角相等,即可得到①中的结论仍然成立; (2)先过点A作AG⊥AC交BC于点G,画出符合要求的图形,再结合图...
练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
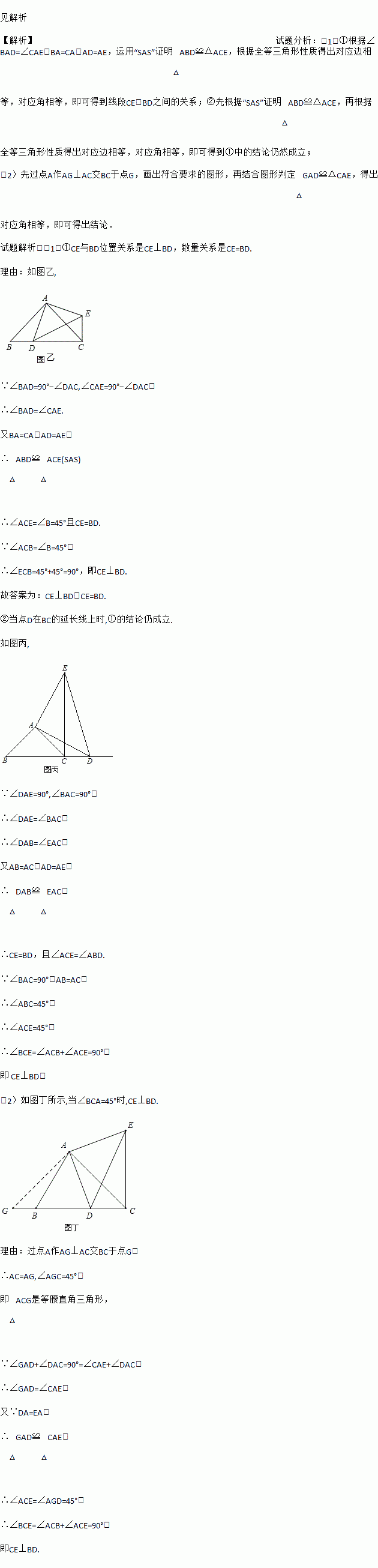

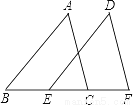
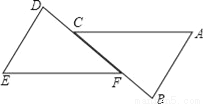
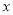 的分式方程
的分式方程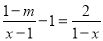 的解是正数,则
的解是正数,则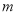 的取值范围是( )
的取值范围是( )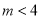 且
且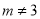 B.
B. 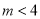
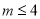 且
且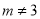 D.
D. 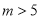 且
且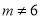
 的值为0,则
的值为0,则 的值为( )
的值为( )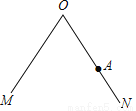

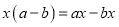 B.
B. 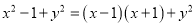
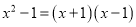 D.
D.