题目内容
16．在AB两地之间要修一条笔直的公路，从A地测得公路的走向是南偏西56°，此工程由甲乙丙三支施工队伍共同建设．已知甲单独做要10天完成，乙单独做要12天完成，丙单独做要15天完成．甲、丙先合做了3天后，甲因事离去，由乙和丙完成剩下工作，那么还需要几天才能完成？并画出这条公路的简单示意图．分析 先建立方位图，再设由乙和丙完成剩下工作，那么还需要x天才能完成，根据题意列出方程，即可解答．
解答 解：如图，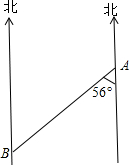
设由乙和丙完成剩下工作，那么还需要x天才能完成，
根据题意得：$（\frac{1}{10}+\frac{1}{15}）×3+（\frac{1}{12}+\frac{1}{15}）x=1$，
解得：x=$\frac{10}{3}$．
∴由乙和丙完成剩下工作，那么还需要$\frac{10}{3}$天才能完成．
点评 本题考查方向角，解决本题的关键是画出方位图，根据题意，列出方程．
练习册系列答案
相关题目
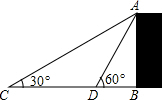某中学初三年级的学生开展测量物体高度的实践活动，他们要测量一幢建筑物AB的高度．如图，他们先在点C处测得建筑物AB的顶点A的仰角为30°，然后向建筑物AB前进10m到达点D处，又测得点A的仰角为60°，那么建筑物AB的高度是5$\sqrt{3}$m．
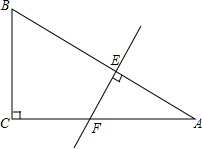如图，在△ABC中，∠C=90°，∠A=22.5°，AB的垂直平分线交AC于F，交AB于E，若CF=3cm，求BC的长．
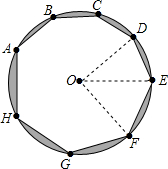同圆或等圆中，圆心角互余的两个扇形叫做互余共轭扇形．如图⊙O内接八边形中，已知AB=BC=CD=DE=2，EF=FG=GH=HA=2$\sqrt{2}$．
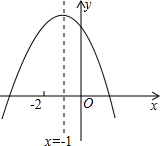已知二次函数y=ax2+bx=c的图象如图，下列结论：
6．为了了解500名初三毕业班学生一分钟跳绳次数的情况，某校抽取了一部分初三毕业生进行一分钟跳绳次数的测试，将所得数据进行处理，可得频率分布表：
（1）这个问题中，总体是初三毕业班学生一分钟跳绳次数的情况的全体；样本容量a=100；
（2）第四小组的频数b=39，频率c=0.39；
（3）若次数在110次（含110次）以上为达标，试估计该校初三毕业生一分钟跳绳的达标率是多少？
| 组别 | 分组 | 频数 | 频率 |
| 1 | 89.5～99.5 | 4 | 0.04 |
| 2 | 99.5～109.5 | 3 | 0.03 |
| 3 | 109.5～119.5 | 46 | 0.46 |
| 4 | 119.5～129.5 | B | c |
| 5 | 129.5～139.5 | 6 | 0.06 |
| 6 | 139.5～149.5 | 2 | 0.02 |
| 合计 | a | 1.00 | |
（2）第四小组的频数b=39，频率c=0.39；
（3）若次数在110次（含110次）以上为达标，试估计该校初三毕业生一分钟跳绳的达标率是多少？